Parsing Expressions
Ngữ pháp, thứ có thể kiểm soát cả các vị vua.
Molière
Chương này đánh dấu cột mốc lớn đầu tiên của cuốn sách. Nhiều người trong chúng ta từng chắp vá một mớ hỗn độn các biểu thức chính quy và thao tác chuỗi con để cố gắng moi ra chút ý nghĩa từ một đống văn bản. Đoạn code đó có lẽ đầy rẫy lỗi và cực khó bảo trì. Việc viết một parser “xịn” — có xử lý lỗi tử tế, cấu trúc nội bộ mạch lạc, và khả năng xử lý vững vàng một cú pháp phức tạp — được xem là một kỹ năng hiếm và ấn tượng. Trong chương này, bạn sẽ đạt được nó.
Nó dễ hơn bạn nghĩ, một phần vì ta đã “gánh” trước khá nhiều việc khó trong chương trước. Bạn đã quen thuộc với ngữ pháp hình thức. Bạn đã biết về syntax tree, và ta đã có sẵn một số class Java để biểu diễn chúng. Mảnh ghép duy nhất còn thiếu là parsing — biến đổi một chuỗi token thành một trong những syntax tree đó.
Một số giáo trình khoa học máy tính rất coi trọng parser. Vào thập niên 60, các nhà khoa học máy tính — vốn đã quá mệt mỏi với việc lập trình bằng hợp ngữ — bắt đầu thiết kế những ngôn ngữ tinh vi hơn, thân thiện hơn với con người như Fortran và ALGOL. Tiếc là, chúng lại không mấy “thân thiện” với máy tính nguyên thủy thời đó.
Những người tiên phong này đã thiết kế ra các ngôn ngữ mà chính họ cũng không chắc làm sao để viết compiler cho chúng, rồi thực hiện những công trình đột phá, phát minh ra các kỹ thuật parsing và compiling có thể xử lý những ngôn ngữ lớn mới mẻ này trên những cỗ máy nhỏ bé, cũ kỹ.
Những cuốn sách compiler kinh điển thường viết như những bản “thánh ca” ca ngợi các anh hùng và công cụ của họ. Bìa cuốn Compilers: Principles, Techniques, and Tools thậm chí còn vẽ một con rồng mang nhãn “độ phức tạp của thiết kế compiler” bị một hiệp sĩ cầm kiếm và khiên khắc chữ “LALR parser generator” và “syntax directed translation” hạ gục. Họ thực sự “đẩy” sự tôn vinh này lên cao.
Một chút tự khen là xứng đáng, nhưng sự thật là bạn không cần biết hầu hết những thứ đó để viết ra một parser chất lượng cao cho máy tính hiện đại. Như mọi khi, tôi khuyến khích bạn mở rộng kiến thức và tìm hiểu thêm sau này, nhưng cuốn sách này sẽ bỏ qua “tủ trưng bày cúp”.
6 . 1Sự mơ hồ & “trò chơi” Parsing
Trong chương trước, tôi đã nói bạn có thể “chơi” một ngữ pháp phi ngữ cảnh như một trò chơi để tạo ra chuỗi. Parser thì chơi trò đó theo hướng ngược lại. Cho một chuỗi — một dãy token — ta ánh xạ các token đó tới các terminal trong ngữ pháp để tìm ra những quy tắc nào có thể đã tạo ra chuỗi đó.
Phần “có thể” này khá thú vị. Hoàn toàn có thể tạo ra một ngữ pháp mơ hồ, nơi các lựa chọn production khác nhau có thể dẫn đến cùng một chuỗi. Khi bạn dùng ngữ pháp để tạo chuỗi, điều đó không quan trọng lắm. Một khi đã có chuỗi, ai quan tâm bạn tạo ra nó bằng cách nào?
Khi parsing, sự mơ hồ đồng nghĩa với việc parser có thể hiểu sai code của người dùng. Khi parse, ta không chỉ xác định xem chuỗi đó có phải code Lox hợp lệ hay không, mà còn theo dõi quy tắc nào khớp với phần nào của nó để biết mỗi token thuộc về phần nào của ngôn ngữ. Đây là ngữ pháp biểu thức Lox mà ta đã xây dựng ở chương trước:
expression → literal | unary | binary | grouping ; literal → NUMBER | STRING | "true" | "false" | "nil" ; grouping → "(" expression ")" ; unary → ( "-" | "!" ) expression ; binary → expression operator expression ; operator → "==" | "!=" | "<" | "<=" | ">" | ">=" | "+" | "-" | "*" | "/" ;
Đây là một chuỗi hợp lệ trong ngữ pháp đó:

Nhưng có hai cách ta có thể đã tạo ra nó. Một cách là:
- Bắt đầu từ
expression, chọnbinary. - Với
expressionbên trái, chọnNUMBERvà dùng6. - Với operator, chọn
"/". - Với
expressionbên phải, lại chọnbinary. - Trong
binarylồng này, chọn3 - 1.
Cách khác:
- Bắt đầu từ
expression, chọnbinary. - Với
expressionbên trái, lại chọnbinary. - Trong
binarylồng này, chọn6 / 3. - Quay lại
binarybên ngoài, với operator, chọn"-". - Với
expressionbên phải, chọnNUMBERvà dùng1.
Chúng tạo ra cùng một chuỗi, nhưng không phải cùng một syntax tree:
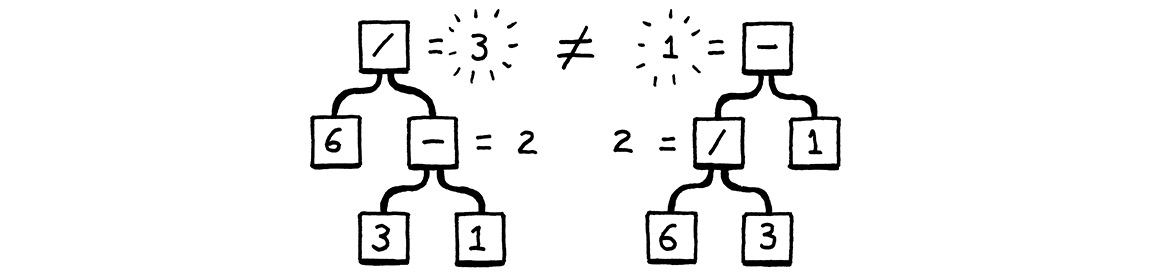
Nói cách khác, ngữ pháp này cho phép ta nhìn biểu thức dưới dạng (6 / 3) - 1 hoặc 6 / (3 - 1). Quy tắc binary cho phép các toán hạng được lồng vào nhau theo bất kỳ cách nào bạn muốn. Điều đó sẽ ảnh hưởng trực tiếp đến kết quả khi đánh giá cây cú pháp đã parse. Cách mà các nhà toán học đã giải quyết sự mơ hồ này từ khi bảng đen mới ra đời là định nghĩa các quy tắc về độ ưu tiên (precedence) và tính kết hợp (associativity).
-
Precedence (độ ưu tiên) xác định toán tử nào được tính trước trong một biểu thức chứa nhiều loại toán tử khác nhau. Quy tắc precedence cho ta biết rằng trong ví dụ trên, ta sẽ tính
/trước-. Toán tử có độ ưu tiên cao hơn sẽ được tính trước toán tử có độ ưu tiên thấp hơn. Nói cách khác, toán tử có độ ưu tiên cao hơn được gọi là “ràng buộc chặt hơn” (bind tighter). -
Associativity (tính kết hợp) xác định toán tử nào được tính trước trong một chuỗi các toán tử giống nhau. Khi một toán tử là left-associative (kết hợp trái, hiểu là “từ trái sang phải”), các toán tử bên trái sẽ được tính trước các toán tử bên phải. Vì
-là left-associative, biểu thức:5 - 3 - 1
tương đương với:
(5 - 3) - 1
Ngược lại, phép gán (assignment) là right-associative (kết hợp phải). Biểu thức:
a = b = c
tương đương với:
a = (b = c)
Nếu không có quy tắc precedence và associativity được định nghĩa rõ ràng, một biểu thức dùng nhiều toán tử sẽ trở nên mơ hồ — nó có thể được parse thành các cây cú pháp khác nhau, và từ đó cho ra các kết quả khác nhau khi đánh giá. Ta sẽ khắc phục điều này trong Lox bằng cách áp dụng cùng quy tắc precedence như C, từ thấp đến cao.
| Name | Operators | Associates |
| Equality | == != |
Left |
| Comparison | > >=
< <= |
Left |
| Term | - + |
Left |
| Factor | / * |
Left |
| Unary | ! - |
Right |
Hiện tại, ngữ pháp đang nhồi tất cả các loại biểu thức vào chung một quy tắc expression. Quy tắc này cũng được dùng làm non-terminal cho các toán hạng, điều này khiến ngữ pháp chấp nhận bất kỳ loại biểu thức nào làm biểu thức con, bất kể quy tắc precedence có cho phép hay không.
Ta sẽ sửa điều đó bằng cách phân tầng ngữ pháp. Ta định nghĩa một quy tắc riêng cho mỗi mức precedence.
expression → ... equality → ... comparison → ... term → ... factor → ... unary → ... primary → ...
Mỗi quy tắc ở đây chỉ khớp với các biểu thức ở mức precedence của nó hoặc cao hơn. Ví dụ, unary khớp với một biểu thức unary như !negated hoặc một biểu thức primary như 1234. Còn term có thể khớp 1 + 2 nhưng cũng có thể khớp 3 * 4 / 5. Quy tắc primary cuối cùng bao phủ các dạng có precedence cao nhất — literal và biểu thức trong ngoặc.
Giờ ta chỉ cần điền các production cho từng quy tắc đó. Ta sẽ làm các quy tắc dễ trước. Quy tắc expression ở trên cùng khớp với bất kỳ biểu thức nào ở bất kỳ mức precedence nào. Vì equality có precedence thấp nhất, nếu ta khớp được nó thì nó sẽ bao trùm tất cả.
expression → equality
Ở đầu kia của bảng precedence, một biểu thức primary chứa tất cả literal và biểu thức nhóm trong ngoặc.
primary → NUMBER | STRING | "true" | "false" | "nil" | "(" expression ")" ;
Một biểu thức unary bắt đầu bằng một toán tử unary theo sau là toán hạng. Vì toán tử unary có thể lồng nhau — !!true là một biểu thức hợp lệ dù hơi kỳ — nên toán hạng cũng có thể lại là một toán tử unary. Quy tắc đệ quy xử lý điều này rất gọn.
unary → ( "!" | "-" ) unary ;
Nhưng quy tắc này có vấn đề: nó sẽ không bao giờ kết thúc.
Hãy nhớ, mỗi quy tắc cần khớp với các biểu thức ở mức precedence đó hoặc cao hơn, nên ta cũng cần cho phép nó khớp với một biểu thức primary.
unary → ( "!" | "-" ) unary | primary ;
Vậy là ổn.
Các quy tắc còn lại đều là toán tử nhị phân. Ta sẽ bắt đầu với quy tắc cho phép nhân và chia. Đây là thử đầu tiên:
factor → factor ( "/" | "*" ) unary | unary ;
Quy tắc này đệ quy để khớp toán hạng bên trái. Điều đó cho phép quy tắc khớp một chuỗi các phép nhân và chia như 1 * 2 / 3. Đặt production đệ quy ở bên trái và unary ở bên phải khiến quy tắc này left-associative và không mơ hồ.
Tất cả những điều này đều đúng, nhưng việc ký hiệu đầu tiên trong thân quy tắc giống với ký hiệu ở đầu quy tắc nghĩa là production này left-recursive. Một số kỹ thuật parsing, bao gồm cả kỹ thuật ta sẽ dùng, gặp khó khăn với left recursion. (Đệ quy ở chỗ khác, như trong unary và đệ quy gián tiếp cho grouping trong primary, thì không vấn đề gì.)
Có nhiều ngữ pháp bạn có thể định nghĩa để khớp cùng một ngôn ngữ. Việc chọn cách mô hình hóa một ngôn ngữ cụ thể vừa là vấn đề sở thích, vừa là vấn đề thực dụng. Quy tắc này đúng, nhưng không tối ưu cho cách ta định parse nó. Thay vì dùng quy tắc left-recursive, ta sẽ dùng một quy tắc khác.
factor → unary ( ( "/" | "*" ) unary )* ;
Ta định nghĩa một biểu thức factor là một chuỗi phẳng các phép nhân và chia. Quy tắc này khớp cùng cú pháp với quy tắc trước, nhưng phản ánh tốt hơn cấu trúc code ta sẽ viết để parse Lox. Ta sẽ dùng cùng cấu trúc này cho tất cả các mức precedence của toán tử nhị phân khác, cho ta toàn bộ ngữ pháp biểu thức hoàn chỉnh như sau:
expression → equality ; equality → comparison ( ( "!=" | "==" ) comparison )* ; comparison → term ( ( ">" | ">=" | "<" | "<=" ) term )* ; term → factor ( ( "-" | "+" ) factor )* ; factor → unary ( ( "/" | "*" ) unary )* ; unary → ( "!" | "-" ) unary | primary ; primary → NUMBER | STRING | "true" | "false" | "nil" | "(" expression ")" ;
Ngữ pháp này phức tạp hơn so với cái ta có trước đây, nhưng đổi lại, ta đã loại bỏ được sự mơ hồ của ngữ pháp cũ. Đây chính là thứ ta cần để tạo ra một parser.
6 . 2Recursive Descent Parsing
Có cả một “bầy” kỹ thuật parsing với tên gọi chủ yếu là sự kết hợp của các chữ “L” và “R” — LL(k), LR(1), LALR — cùng với những “sinh vật” kỳ lạ hơn như parser combinators, Earley parsers, thuật toán shunting yard, và packrat parsing. Với interpreter đầu tiên của chúng ta, chỉ một kỹ thuật là quá đủ: recursive descent.
Recursive descent là cách đơn giản nhất để xây dựng một parser, và không cần dùng đến các công cụ parser generator phức tạp như Yacc, Bison hay ANTLR. Tất cả những gì bạn cần là code viết tay đơn giản, rõ ràng. Nhưng đừng để sự đơn giản đó đánh lừa bạn. Parser kiểu recursive descent nhanh, ổn định, và có thể hỗ trợ xử lý lỗi tinh vi. Thực tế, GCC, V8 (JavaScript VM trong Chrome), Roslyn (C# compiler viết bằng C#) và nhiều hiện thực ngôn ngữ “hạng nặng” khác đều dùng recursive descent. Nó thực sự rất “đỉnh”.
Recursive descent được coi là một top-down parser vì nó bắt đầu từ quy tắc ngữ pháp cao nhất hoặc ngoài cùng (ở đây là expression) và lần lượt đi xuống các biểu thức con lồng nhau trước khi cuối cùng chạm tới các lá của syntax tree. Điều này trái ngược với các parser bottom-up như LR, vốn bắt đầu từ các biểu thức primary và ghép chúng thành các khối cú pháp lớn dần.
Một recursive descent parser là bản dịch gần như nguyên văn các quy tắc ngữ pháp sang code mệnh lệnh. Mỗi quy tắc trở thành một hàm. Phần thân của quy tắc được dịch thành code có dạng gần như sau:
| Grammar notation | Code representation |
| Terminal | Code to match and consume a token |
| Nonterminal | Call to that rule’s function |
| | if or switch statement |
* or + | while or for loop |
? | if statement |
Việc “descent” (đi xuống) được gọi là “recursive” (đệ quy) vì khi một quy tắc ngữ pháp tham chiếu tới chính nó — trực tiếp hoặc gián tiếp — điều đó sẽ được dịch thành một lời gọi hàm đệ quy.
6 . 2 . 1Lớp parser
Mỗi quy tắc ngữ pháp sẽ trở thành một phương thức bên trong lớp mới này:
create new file
package com.craftinginterpreters.lox; import java.util.List; import static com.craftinginterpreters.lox.TokenType.*; class Parser { private final List<Token> tokens; private int current = 0; Parser(List<Token> tokens) { this.tokens = tokens; } }
Giống như scanner, parser tiêu thụ một chuỗi đầu vào phẳng, chỉ khác là giờ ta đang đọc token thay vì ký tự. Ta lưu danh sách token và dùng biến current để trỏ tới token tiếp theo đang chờ được parse.
Giờ ta sẽ đi thẳng qua toàn bộ ngữ pháp biểu thức và dịch từng quy tắc sang code Java. Quy tắc đầu tiên, expression, đơn giản chỉ mở rộng thành quy tắc equality, nên khá dễ dàng.
add after Parser()
private Expr expression() { return equality(); }
Mỗi phương thức parse một quy tắc ngữ pháp sẽ tạo ra một syntax tree cho quy tắc đó và trả về cho hàm gọi nó. Khi phần thân của quy tắc chứa một nonterminal — tham chiếu tới một quy tắc khác — ta sẽ gọi phương thức của quy tắc đó.
Quy tắc cho equality phức tạp hơn một chút.
equality → comparison ( ( "!=" | "==" ) comparison )* ;
Trong Java, nó trở thành:
add after expression()
private Expr equality() { Expr expr = comparison(); while (match(BANG_EQUAL, EQUAL_EQUAL)) { Token operator = previous(); Expr right = comparison(); expr = new Expr.Binary(expr, operator, right); } return expr; }
Hãy cùng phân tích. Nonterminal comparison đầu tiên trong phần thân được dịch thành lời gọi đầu tiên tới comparison() trong phương thức. Ta lấy kết quả đó và lưu vào một biến cục bộ.
Tiếp theo, vòng lặp ( ... )* trong quy tắc được ánh xạ thành vòng lặp while. Ta cần biết khi nào thì thoát khỏi vòng lặp này. Có thể thấy rằng bên trong quy tắc, trước tiên ta phải tìm thấy một token != hoặc ==. Vậy nên, nếu không thấy một trong số đó, ta biết là đã xong chuỗi các toán tử equality. Ta diễn đạt việc kiểm tra này bằng phương thức tiện lợi match().
add after equality()
private boolean match(TokenType... types) { for (TokenType type : types) { if (check(type)) { advance(); return true; } } return false; }
Phương thức này kiểm tra xem token hiện tại có thuộc một trong các loại được truyền vào hay không. Nếu có, nó tiêu thụ token đó và trả về true. Nếu không, nó trả về false và giữ nguyên token hiện tại. match() được định nghĩa dựa trên hai thao tác cơ bản hơn.
Phương thức check() trả về true nếu token hiện tại có kiểu được chỉ định. Không giống match(), nó không bao giờ tiêu thụ token, chỉ nhìn vào nó.
add after match()
private boolean check(TokenType type) { if (isAtEnd()) return false; return peek().type == type; }
Phương thức advance() tiêu thụ token hiện tại và trả về nó, tương tự như cách phương thức tương ứng của scanner duyệt qua các ký tự.
add after check()
private Token advance() { if (!isAtEnd()) current++; return previous(); }
Các phương thức này dựa trên một vài thao tác nguyên thủy cuối cùng.
add after advance()
private boolean isAtEnd() { return peek().type == EOF; } private Token peek() { return tokens.get(current); } private Token previous() { return tokens.get(current - 1); }
isAtEnd() kiểm tra xem ta đã hết token để parse chưa. peek() trả về token hiện tại mà ta chưa tiêu thụ, và previous() trả về token vừa được tiêu thụ gần nhất. Cái sau giúp ta dễ dàng dùng match() rồi truy cập token vừa khớp.
Đó là hầu hết phần hạ tầng parsing mà ta cần. Ta đang ở đâu nhỉ? À đúng rồi, nếu ta đang ở bên trong vòng lặp while trong equality(), thì ta biết mình vừa tìm thấy một toán tử != hoặc == và phải parse một biểu thức equality.
Ta lấy token toán tử vừa khớp để biết mình đang xử lý loại biểu thức equality nào. Sau đó ta gọi lại comparison() để parse toán hạng bên phải. Ta kết hợp toán tử và hai toán hạng của nó thành một node syntax tree Expr.Binary mới, rồi quay lại vòng lặp. Mỗi vòng lặp, ta lưu biểu thức kết quả vào lại biến cục bộ expr. Khi ta duyệt qua một chuỗi các biểu thức equality, điều này sẽ tạo ra một cây lồng nhau theo kiểu left-associative gồm các node toán tử nhị phân.
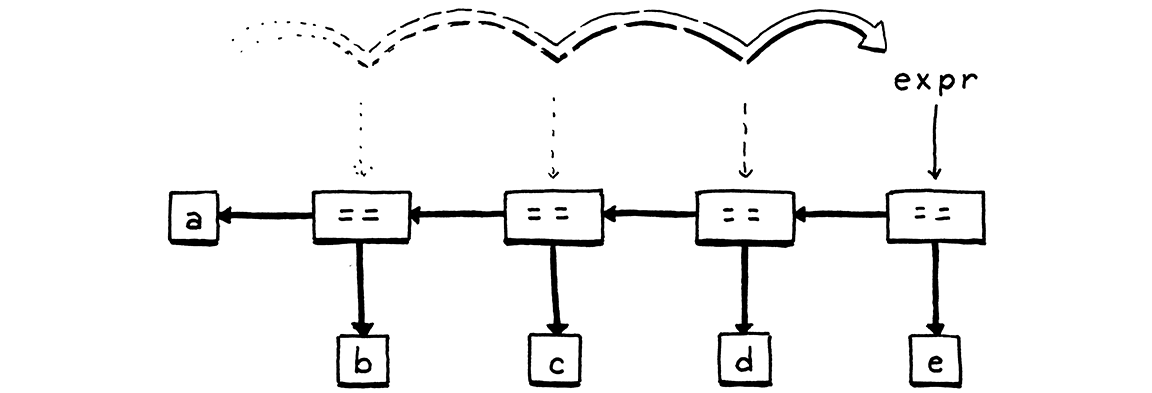
Parser sẽ thoát khỏi vòng lặp ngay khi gặp một token không phải là toán tử equality. Cuối cùng, nó trả về biểu thức. Lưu ý rằng nếu parser không bao giờ gặp toán tử equality, nó sẽ không bao giờ vào vòng lặp. Trong trường hợp đó, phương thức equality() thực chất chỉ gọi và trả về comparison(). Theo cách này, phương thức này sẽ khớp một toán tử equality hoặc bất kỳ thứ gì có precedence cao hơn.
Chuyển sang quy tắc tiếp theo . . .
comparison → term ( ( ">" | ">=" | "<" | "<=" ) term )* ;
Dịch sang Java:
add after equality()
private Expr comparison() { Expr expr = term(); while (match(GREATER, GREATER_EQUAL, LESS, LESS_EQUAL)) { Token operator = previous(); Expr right = term(); expr = new Expr.Binary(expr, operator, right); } return expr; }
Quy tắc ngữ pháp này gần như giống hệt equality và code tương ứng cũng vậy. Điểm khác biệt duy nhất là loại token của các toán tử cần khớp, và phương thức ta gọi cho các toán hạng — giờ là term() thay vì comparison(). Hai quy tắc còn lại cho toán tử nhị phân cũng theo cùng một mẫu.
Theo thứ tự precedence, trước tiên là cộng và trừ:
add after comparison()
private Expr term() { Expr expr = factor(); while (match(MINUS, PLUS)) { Token operator = previous(); Expr right = factor(); expr = new Expr.Binary(expr, operator, right); } return expr; }
Và cuối cùng là nhân và chia:
add after term()
private Expr factor() { Expr expr = unary(); while (match(SLASH, STAR)) { Token operator = previous(); Expr right = unary(); expr = new Expr.Binary(expr, operator, right); } return expr; }
Vậy là xong các toán tử nhị phân, được parse với precedence và associativity chính xác. Ta đang dần leo lên bậc thang precedence và giờ đã tới toán tử unary.
unary → ( "!" | "-" ) unary | primary ;
Code cho phần này hơi khác một chút.
add after factor()
private Expr unary() { if (match(BANG, MINUS)) { Token operator = previous(); Expr right = unary(); return new Expr.Unary(operator, right); } return primary(); }
Một lần nữa, ta nhìn vào token hiện tại để quyết định cách parse. Nếu nó là ! hoặc -, chắc chắn ta đang có một biểu thức unary. Khi đó, ta lấy token này rồi đệ quy gọi lại unary() để parse toán hạng. Gói tất cả lại thành một node syntax tree unary expression là xong.
Nếu không, nghĩa là ta đã tới mức precedence cao nhất — các biểu thức primary.
primary → NUMBER | STRING | "true" | "false" | "nil" | "(" expression ")" ;
Hầu hết các trường hợp trong quy tắc này là terminal đơn, nên việc parse khá đơn giản.
add after unary()
private Expr primary() { if (match(FALSE)) return new Expr.Literal(false); if (match(TRUE)) return new Expr.Literal(true); if (match(NIL)) return new Expr.Literal(null); if (match(NUMBER, STRING)) { return new Expr.Literal(previous().literal); } if (match(LEFT_PAREN)) { Expr expr = expression(); consume(RIGHT_PAREN, "Expect ')' after expression."); return new Expr.Grouping(expr); } }
Nhánh thú vị là phần xử lý dấu ngoặc. Sau khi khớp dấu ( mở và parse biểu thức bên trong, ta phải tìm thấy token ) đóng. Nếu không, đó là lỗi.
6 . 3Lỗi cú pháp (Syntax Errors)
Một parser thực sự có hai nhiệm vụ:
-
Với một chuỗi token hợp lệ, tạo ra syntax tree tương ứng.
-
Với một chuỗi token không hợp lệ, phát hiện lỗi và thông báo cho người dùng về sai sót của họ.
Đừng đánh giá thấp tầm quan trọng của nhiệm vụ thứ hai! Trong các IDE và trình soạn thảo hiện đại, parser liên tục parse lại code — thường là khi người dùng vẫn đang gõ — để tô sáng cú pháp và hỗ trợ các tính năng như auto-complete. Điều đó có nghĩa là nó sẽ gặp code ở trạng thái chưa hoàn chỉnh, sai một nửa liên tục.
Khi người dùng không nhận ra cú pháp đang sai, parser phải giúp họ quay lại đúng hướng. Cách parser báo lỗi là một phần quan trọng trong giao diện người dùng của ngôn ngữ. Xử lý lỗi cú pháp tốt là việc khó. Theo định nghĩa, code đang ở trạng thái không rõ ràng, nên không có cách nào chắc chắn biết được người dùng định viết gì. Parser không thể đọc được tâm trí của bạn.
Có một vài yêu cầu bắt buộc khi parser gặp lỗi cú pháp. Một parser phải:
-
Phát hiện và báo lỗi. Nếu nó không phát hiện lỗi và chuyển cây cú pháp sai lệch đó sang cho interpreter, thì đủ loại “kinh dị” có thể xảy ra.
-
Tránh crash hoặc treo. Lỗi cú pháp là chuyện thường tình, và các công cụ ngôn ngữ phải đủ vững để đối mặt với chúng. Việc segfault hoặc mắc kẹt trong vòng lặp vô hạn là không chấp nhận được. Dù source có thể không phải là code hợp lệ, nó vẫn là đầu vào hợp lệ cho parser vì người dùng dùng parser để biết cú pháp nào được phép.
Đó là “vé vào cửa” nếu bạn muốn tham gia “cuộc chơi” parser, nhưng bạn thực sự nên nâng tiêu chuẩn lên hơn thế. Một parser tốt nên:
-
Nhanh. Máy tính ngày nay nhanh hơn hàng nghìn lần so với khi công nghệ parser mới ra đời. Thời kỳ phải tối ưu parser để nó parse xong cả file source trong lúc bạn uống cà phê đã qua. Nhưng kỳ vọng của lập trình viên cũng tăng nhanh không kém, nếu không muốn nói là nhanh hơn. Họ mong editor của mình parse lại file chỉ trong vài mili-giây sau mỗi lần gõ phím.
-
Báo tất cả lỗi riêng biệt. Dừng lại sau lỗi đầu tiên thì dễ lập trình, nhưng sẽ gây khó chịu nếu mỗi lần họ sửa “lỗi duy nhất” trong file, lại xuất hiện một lỗi mới. Họ muốn thấy tất cả.
-
Giảm thiểu lỗi dây chuyền. Khi đã gặp một lỗi, parser thực sự không còn chắc chuyện gì đang diễn ra. Nó cố gắng tự đưa mình về đúng hướng và tiếp tục, nhưng nếu bị rối, nó có thể báo ra một loạt lỗi “ma” không phản ánh vấn đề thực sự nào khác trong code. Khi lỗi đầu tiên được sửa, những “bóng ma” này biến mất, vì chúng chỉ phản ánh sự rối loạn của parser. Lỗi dây chuyền gây khó chịu vì có thể khiến người dùng tưởng code của họ tệ hơn thực tế.
Hai điểm cuối này có phần mâu thuẫn. Ta muốn báo càng nhiều lỗi riêng biệt càng tốt, nhưng không muốn báo những lỗi chỉ là hệ quả của lỗi trước đó.
Cách parser phản ứng với lỗi và tiếp tục tìm các lỗi sau được gọi là error recovery. Đây từng là một chủ đề nghiên cứu nóng vào thập niên 60. Khi đó, bạn sẽ đưa một chồng thẻ đục lỗ cho thư ký và quay lại ngày hôm sau để xem compiler có chạy thành công không. Với vòng lặp lặp lại chậm như vậy, bạn thực sự muốn tìm mọi lỗi trong code chỉ trong một lần chạy.
Ngày nay, khi parser hoàn tất trước cả khi bạn gõ xong, vấn đề này ít nghiêm trọng hơn. Một cơ chế error recovery đơn giản, nhanh là đủ.
6 . 3 . 1Panic mode error recovery
Trong số các kỹ thuật recovery được nghĩ ra từ xưa, kỹ thuật trụ vững nhất theo thời gian được gọi — nghe hơi đáng sợ — là panic mode. Ngay khi parser phát hiện lỗi, nó sẽ vào panic mode. Nó biết ít nhất một token không hợp lý với trạng thái hiện tại của nó trong giữa một đống production của ngữ pháp.
Trước khi có thể parse tiếp, nó cần đưa trạng thái và chuỗi token sắp tới về đồng bộ sao cho token tiếp theo khớp với quy tắc đang parse. Quá trình này gọi là synchronization.
Để làm vậy, ta chọn một quy tắc trong ngữ pháp làm điểm đồng bộ. Parser sẽ chỉnh lại trạng thái parse bằng cách nhảy ra khỏi bất kỳ production lồng nhau nào cho đến khi quay lại quy tắc đó. Sau đó, nó đồng bộ luồng token bằng cách bỏ qua các token cho đến khi gặp một token có thể xuất hiện tại điểm đó trong quy tắc.
Bất kỳ lỗi cú pháp thực sự nào ẩn trong các token bị bỏ qua sẽ không được báo, nhưng điều đó cũng có nghĩa là các lỗi dây chuyền sai lệch do lỗi ban đầu gây ra cũng sẽ không bị báo nhầm, và đây là một sự đánh đổi hợp lý.
Vị trí truyền thống trong ngữ pháp để đồng bộ là giữa các statement. Ta chưa có chúng ở đây, nên trong chương này sẽ chưa thực hiện đồng bộ, nhưng ta sẽ chuẩn bị sẵn cơ chế cho sau này.
6 . 3 . 2Vào panic mode
Trước khi rẽ sang phần error recovery này, ta đang viết code để parse một biểu thức trong ngoặc. Sau khi parse xong biểu thức, parser tìm dấu ) đóng bằng cách gọi consume(). Và đây, cuối cùng, là phương thức đó:
add after match()
private Token consume(TokenType type, String message) { if (check(type)) return advance(); throw error(peek(), message); }
Nó giống match() ở chỗ kiểm tra xem token tiếp theo có đúng kiểu mong đợi không. Nếu có, nó tiêu thụ token đó và mọi thứ đều ổn. Nếu là token khác, tức là ta gặp lỗi. Ta báo lỗi bằng cách gọi:
add after previous()
private ParseError error(Token token, String message) { Lox.error(token, message); return new ParseError(); }
Đầu tiên, hàm này hiển thị lỗi cho người dùng bằng cách gọi:
add after report()
static void error(Token token, String message) { if (token.type == TokenType.EOF) { report(token.line, " at end", message); } else { report(token.line, " at '" + token.lexeme + "'", message); } }
Hàm này báo lỗi tại một token cụ thể. Nó hiển thị vị trí của token và chính token đó. Điều này sẽ hữu ích sau này vì ta dùng token xuyên suốt interpreter để theo dõi vị trí trong code.
Sau khi báo lỗi, người dùng đã biết sai sót của mình, nhưng parser sẽ làm gì tiếp theo? Quay lại error(), ta tạo và trả về một ParseError, một instance của class mới này:
class Parser {
nest inside class Parser
private static class ParseError extends RuntimeException {}
private final List<Token> tokens;
Đây là một sentinel class đơn giản mà ta dùng để “tháo” parser ra. Phương thức error() trả về lỗi thay vì ném nó ra ngoài vì ta muốn để phương thức gọi bên trong parser quyết định có “tháo” hay không. Một số lỗi parse xảy ra ở những nơi parser khó mà rơi vào trạng thái rối, và ta không cần phải synchronize. Ở những chỗ đó, ta chỉ cần báo lỗi và tiếp tục chạy.
Ví dụ, Lox giới hạn số lượng đối số bạn có thể truyền cho một hàm. Nếu bạn truyền quá nhiều, parser cần báo lỗi đó, nhưng nó hoàn toàn có thể và nên tiếp tục parse các đối số thừa thay vì hoảng loạn và vào panic mode.
Trong trường hợp của ta, lỗi cú pháp đủ “xấu” để ta muốn panic và đồng bộ lại. Việc bỏ qua token thì khá dễ, nhưng làm sao để đồng bộ lại trạng thái của chính parser?
6 . 3 . 3Đồng bộ một recursive descent parser
Với recursive descent, trạng thái của parser — tức là nó đang ở giữa việc nhận diện quy tắc nào — không được lưu tường minh trong các field. Thay vào đó, ta dùng chính call stack của Java để theo dõi parser đang làm gì. Mỗi quy tắc đang parse dở là một call frame trên stack. Để đặt lại trạng thái đó, ta cần “dọn” các call frame này.
Cách tự nhiên để làm điều đó trong Java là dùng exception. Khi muốn đồng bộ, ta ném đối tượng ParseError đó. Ở mức cao hơn, trong phương thức của quy tắc ngữ pháp mà ta muốn đồng bộ tới, ta sẽ bắt nó. Vì ta đồng bộ ở ranh giới giữa các statement, nên ta sẽ bắt exception ở đó. Sau khi exception được bắt, parser đã ở trạng thái đúng. Việc còn lại là đồng bộ các token.
Ta muốn bỏ qua token cho đến khi ngay tại đầu của statement tiếp theo. Ranh giới này khá dễ nhận ra — đó là một trong những lý do chính ta chọn nó. Sau dấu chấm phẩy, ta có lẽ đã kết thúc một statement. Hầu hết các statement bắt đầu bằng một keyword — for, if, return, var, v.v. Khi token tiếp theo là một trong số đó, ta có khả năng sắp bắt đầu một statement.
Phương thức này đóng gói logic đó:
add after error()
private void synchronize() { advance(); while (!isAtEnd()) { if (previous().type == SEMICOLON) return; switch (peek().type) { case CLASS: case FUN: case VAR: case FOR: case IF: case WHILE: case PRINT: case RETURN: return; } advance(); } }
Nó bỏ qua token cho đến khi nghĩ rằng đã tìm thấy ranh giới statement. Sau khi bắt ParseError, ta sẽ gọi phương thức này và hy vọng sẽ đồng bộ lại. Khi hoạt động tốt, ta đã bỏ qua các token vốn có khả năng gây ra lỗi dây chuyền, và giờ ta có thể parse phần còn lại của file bắt đầu từ statement tiếp theo.
Tiếc là ta chưa được thấy phương thức này hoạt động, vì ta chưa có statement. Ta sẽ gặp lại nó trong vài chương nữa. Hiện tại, nếu xảy ra lỗi, ta sẽ panic và “tháo” toàn bộ lên trên cùng và dừng parse. Vì ta chỉ parse được một biểu thức duy nhất, nên cũng không mất mát gì nhiều.
6 . 4Kết nối Parser
Giờ ta gần như đã xong phần parse biểu thức. Còn một chỗ nữa cần thêm chút xử lý lỗi. Khi parser đi xuống qua các phương thức parse cho từng quy tắc ngữ pháp, cuối cùng nó sẽ chạm tới primary(). Nếu không có trường hợp nào trong đó khớp, nghĩa là ta đang ở một token không thể bắt đầu một biểu thức. Ta cũng cần xử lý lỗi này.
if (match(LEFT_PAREN)) {
Expr expr = expression();
consume(RIGHT_PAREN, "Expect ')' after expression.");
return new Expr.Grouping(expr);
}
in primary()
throw error(peek(), "Expect expression.");
}
Với điều đó, phần còn lại trong parser chỉ là định nghĩa một phương thức khởi đầu để bắt đầu quá trình. Phương thức đó, tất nhiên, là parse().
add after Parser()
Expr parse() { try { return expression(); } catch (ParseError error) { return null; } }
Ta sẽ quay lại phương thức này sau khi thêm statement vào ngôn ngữ. Hiện tại, nó parse một biểu thức duy nhất và trả về nó. Ta cũng có một chút code tạm thời để thoát khỏi panic mode. Việc khôi phục lỗi cú pháp là nhiệm vụ của parser, nên ta không muốn exception ParseError thoát ra ngoài vào phần còn lại của interpreter.
Khi xảy ra lỗi cú pháp, phương thức này trả về null. Không sao cả. Parser hứa sẽ không crash hoặc treo khi gặp cú pháp không hợp lệ, nhưng nó không hứa sẽ trả về một syntax tree dùng được nếu có lỗi. Ngay khi parser báo lỗi, hadError sẽ được đặt, và các giai đoạn tiếp theo sẽ bị bỏ qua.
Cuối cùng, ta có thể kết nối parser mới tinh này vào lớp Lox chính và thử nó. Ta vẫn chưa có interpreter, nên hiện tại, ta sẽ parse thành syntax tree và dùng lớp AstPrinter từ chương trước để hiển thị nó.
Xóa đoạn code cũ in ra các token đã scan và thay bằng đoạn này:
List<Token> tokens = scanner.scanTokens();
in run()
replace 5 lines
Parser parser = new Parser(tokens); Expr expression = parser.parse(); // Stop if there was a syntax error. if (hadError) return; System.out.println(new AstPrinter().print(expression));
}
Chúc mừng, bạn đã vượt qua ngưỡng cửa! Đó thực sự là tất cả những gì cần để viết tay một parser. Ta sẽ mở rộng ngữ pháp trong các chương sau với phép gán, statement và các thứ khác, nhưng không thứ nào phức tạp hơn các toán tử nhị phân mà ta đã xử lý ở đây.
Chạy interpreter và gõ vài biểu thức. Thấy nó xử lý precedence và associativity chính xác chứ? Không tệ cho chưa tới 200 dòng code.
6 . 5Thử thách
-
Trong C, một block là một dạng statement cho phép bạn gói một loạt statement vào chỗ mà chỉ một statement được mong đợi. Toán tử dấu phẩy là một cú pháp tương tự cho biểu thức. Một chuỗi biểu thức được phân tách bằng dấu phẩy có thể được đặt ở nơi chỉ mong đợi một biểu thức (ngoại trừ bên trong danh sách đối số của lời gọi hàm). Khi chạy, toán tử dấu phẩy sẽ tính toán toán hạng bên trái và bỏ kết quả. Sau đó nó tính toán và trả về toán hạng bên phải.
Thêm hỗ trợ cho biểu thức dấu phẩy. Cho chúng cùng precedence và associativity như trong C. Viết ngữ pháp, rồi hiện thực code parsing cần thiết.
-
Tương tự, thêm hỗ trợ cho toán tử điều kiện kiểu C hay còn gọi là toán tử “ternary”
?:. Mức precedence nào được phép giữa?và:? Toàn bộ toán tử này là left-associative hay right-associative? -
Thêm error production để xử lý trường hợp mỗi toán tử nhị phân xuất hiện mà không có toán hạng bên trái. Nói cách khác, phát hiện toán tử nhị phân xuất hiện ở đầu một biểu thức. Báo đó là lỗi, nhưng cũng parse và bỏ qua toán hạng bên phải với precedence phù hợp.
6 . 6Ghi chú thiết kế: Logic & Lịch sử
Giả sử ta quyết định thêm các toán tử bitwise & và | vào Lox. Ta nên đặt chúng ở đâu trong bảng precedence? C — và hầu hết các ngôn ngữ đi theo bước chân của C — đặt chúng dưới ==. Điều này được xem là một sai lầm vì nó khiến các thao tác phổ biến như kiểm tra cờ (flag) cần phải có ngoặc.
if (flags & FLAG_MASK == SOME_FLAG) { ... } // Sai. if ((flags & FLAG_MASK) == SOME_FLAG) { ... } // Đúng.
Ta có nên sửa điều này cho Lox và đặt các toán tử bitwise cao hơn trong bảng precedence so với C không? Có hai chiến lược ta có thể áp dụng.
Bạn hầu như không bao giờ muốn dùng kết quả của một biểu thức == làm toán hạng cho một toán tử bitwise. Bằng cách làm cho bitwise “ràng buộc chặt” hơn, người dùng sẽ ít phải thêm ngoặc hơn. Vậy nếu ta làm vậy, và người dùng giả định precedence được chọn một cách hợp lý để giảm ngoặc, họ sẽ có khả năng suy ra đúng.
Sự nhất quán nội tại kiểu này giúp ngôn ngữ dễ học hơn vì có ít trường hợp ngoại lệ và tình huống đặc biệt mà người dùng phải vấp phải rồi sửa. Điều này tốt, vì trước khi người dùng có thể dùng ngôn ngữ của ta, họ phải “nạp” toàn bộ cú pháp và ngữ nghĩa đó vào đầu. Một ngôn ngữ đơn giản, hợp lý hơn có lý.
Nhưng, với nhiều người dùng, còn có một lối tắt nhanh hơn để đưa ý tưởng của ngôn ngữ ta vào “bộ não ướt” của họ — dùng những khái niệm họ đã biết. Nhiều người mới đến với ngôn ngữ của ta sẽ xuất phát từ một hoặc nhiều ngôn ngữ khác. Nếu ngôn ngữ của ta dùng cùng một số cú pháp hoặc ngữ nghĩa với những ngôn ngữ đó, người dùng sẽ phải học (và bỏ học) ít hơn.
Điều này đặc biệt hữu ích với cú pháp. Có thể giờ bạn không nhớ rõ, nhưng khi mới học ngôn ngữ lập trình đầu tiên, code có lẽ trông xa lạ và khó tiếp cận. Chỉ qua nỗ lực kiên trì bạn mới học được cách đọc và chấp nhận nó. Nếu bạn thiết kế một cú pháp mới hoàn toàn cho ngôn ngữ của mình, bạn đang buộc người dùng bắt đầu lại quá trình đó từ đầu.
Tận dụng những gì người dùng đã biết là một trong những công cụ mạnh nhất bạn có thể dùng để giúp ngôn ngữ của mình được chấp nhận. Gần như không thể đánh giá quá cao giá trị của điều này. Nhưng nó cũng đặt bạn trước một vấn đề khó chịu: Điều gì xảy ra khi thứ mà người dùng nào cũng biết lại hơi tệ? Precedence của toán tử bitwise trong C là một sai lầm vô lý. Nhưng đó lại là một sai lầm quen thuộc mà hàng triệu người đã quen và chấp nhận.
Bạn sẽ trung thành với logic nội tại của ngôn ngữ mình và bỏ qua lịch sử? Bạn sẽ bắt đầu từ con số 0 và các nguyên tắc cơ bản? Hay bạn sẽ dệt ngôn ngữ của mình vào tấm thảm phong phú của lịch sử lập trình và giúp người dùng có lợi thế bằng cách bắt đầu từ thứ họ đã biết?
Không có câu trả lời hoàn hảo ở đây, chỉ có sự đánh đổi. Bạn và tôi rõ ràng thiên về việc thích những ngôn ngữ mới mẻ, nên xu hướng tự nhiên là “đốt sách sử” và bắt đầu câu chuyện của riêng mình.
Trong thực tế, thường tốt hơn là tận dụng tối đa những gì người dùng đã biết. Đưa họ đến với ngôn ngữ của bạn là một bước nhảy lớn. Khoảng cách đó càng nhỏ, càng nhiều người sẵn sàng bước qua. Nhưng bạn cũng không thể luôn bám vào lịch sử, nếu không ngôn ngữ của bạn sẽ chẳng có gì mới mẻ và hấp dẫn để cho họ một lý do để nhảy sang.