Representing Code
Với những người sống trong rừng, hầu như mỗi loài cây đều có giọng nói cũng như hình dáng riêng của nó.
Thomas Hardy, Under the Greenwood Tree
Trong chương trước, ta đã lấy mã nguồn thô dưới dạng một chuỗi và biến đổi nó thành một dạng biểu diễn ở mức cao hơn một chút: một chuỗi các token. Parser mà ta sẽ viết trong chương tiếp theo sẽ tiếp tục biến đổi các token đó, thành một dạng biểu diễn còn phong phú và phức tạp hơn nữa.
Trước khi có thể tạo ra dạng biểu diễn đó, ta cần định nghĩa nó. Đó chính là chủ đề của chương này. Trên đường đi, ta sẽ đề cập đến một chút lý thuyết về ngữ pháp hình thức, cảm nhận sự khác biệt giữa lập trình hàm và lập trình hướng đối tượng, điểm qua một vài mẫu thiết kế, và làm một chút metaprogramming.
Trước khi làm tất cả những điều đó, hãy tập trung vào mục tiêu chính — một dạng biểu diễn cho code. Nó cần đơn giản để parser tạo ra và dễ dàng để interpreter tiêu thụ. Nếu bạn chưa từng viết parser hay interpreter, những yêu cầu này có thể chưa rõ ràng lắm. Có lẽ trực giác của bạn sẽ giúp được. Bộ não bạn làm gì khi đóng vai một interpreter… bằng xương bằng thịt? Bạn sẽ đánh giá một biểu thức số học như thế này trong đầu ra sao:
1 + 2 * 3 - 4
Bởi vì bạn hiểu thứ tự thực hiện phép toán — kiểu “Please Excuse My Dear Aunt Sally” — bạn biết rằng phép nhân sẽ được tính trước phép cộng hoặc trừ. Một cách để hình dung precedence đó là dùng một cây. Các node lá là số, và các node bên trong là toán tử với các nhánh trỏ tới từng toán hạng của chúng.
Để tính giá trị của một node phép toán, bạn cần biết giá trị số của các cây con, nên bạn phải tính chúng trước. Điều đó có nghĩa là làm việc từ lá lên gốc — một phép duyệt hậu tự (post-order):
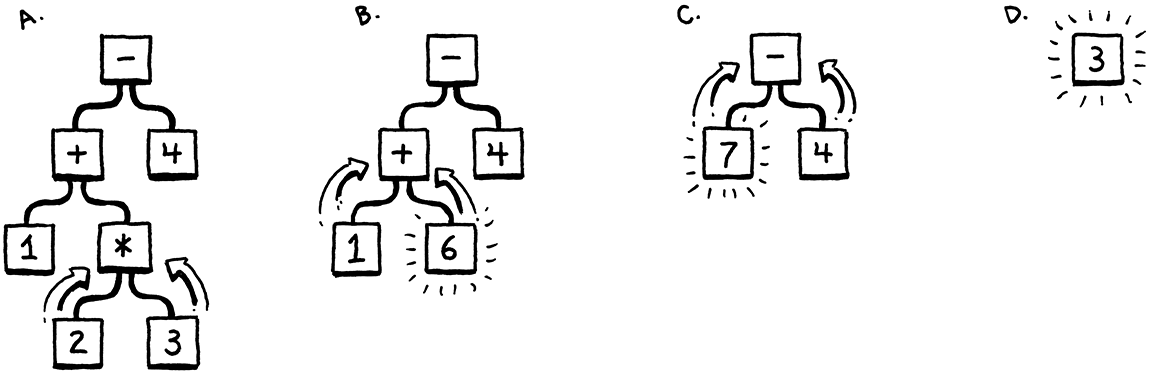
Nếu tôi đưa cho bạn một biểu thức số học, bạn có thể dễ dàng vẽ ra một trong những cây này. Và khi đã có cây, bạn có thể tính toán nó một cách nhẹ nhàng. Vậy nên, một cách trực giác, có vẻ như một dạng biểu diễn hợp lý cho code của ta là một cây khớp với cấu trúc ngữ pháp — sự lồng nhau của các toán tử — của ngôn ngữ.
Vậy ta cần xác định chính xác hơn ngữ pháp đó là gì. Giống như ngữ pháp từ vựng ở chương trước, có cả một “núi” lý thuyết xoay quanh ngữ pháp cú pháp. Ta sẽ đi sâu vào lý thuyết này hơn một chút so với khi làm phần scanning, vì nó hóa ra lại là một công cụ hữu ích trong nhiều phần của interpreter. Ta bắt đầu bằng cách tiến lên một bậc trong phân cấp Chomsky . . .
5 . 1Ngữ pháp phi ngữ cảnh (Context-Free Grammars)
Trong chương trước, hình thức mà ta dùng để định nghĩa ngữ pháp từ vựng — các quy tắc về cách ký tự được nhóm thành token — được gọi là ngôn ngữ chính quy (regular language). Điều đó là đủ cho scanner của ta, vốn tạo ra một chuỗi token phẳng. Nhưng ngôn ngữ chính quy không đủ mạnh để xử lý các biểu thức có thể lồng nhau sâu tùy ý.
Ta cần một “cây búa” to hơn, và cây búa đó là ngữ pháp phi ngữ cảnh (CFG). Đây là công cụ nặng ký tiếp theo trong hộp đồ nghề của ngữ pháp hình thức. Một ngữ pháp hình thức lấy một tập hợp các thành phần nguyên tử gọi là “bảng chữ cái” (alphabet). Sau đó nó định nghĩa một tập hợp (thường là vô hạn) các “chuỗi” thuộc ngữ pháp. Mỗi chuỗi là một dãy “chữ cái” trong bảng chữ cái.
Tôi để tất cả những từ đó trong dấu ngoặc kép vì các thuật ngữ này có thể gây nhầm lẫn khi bạn chuyển từ ngữ pháp từ vựng sang ngữ pháp cú pháp. Trong ngữ pháp của scanner, bảng chữ cái gồm các ký tự riêng lẻ và các chuỗi là những lexeme hợp lệ — gần giống như “từ”. Trong ngữ pháp cú pháp mà ta đang nói tới bây giờ, ta ở một mức độ chi tiết khác. Giờ mỗi “chữ cái” trong bảng chữ cái là cả một token, và một “chuỗi” là một dãy token — tức là cả một biểu thức.
Ôi. Có lẽ một bảng so sánh sẽ giúp:
| Terminology | Lexical grammar | Syntactic grammar | |
| The “alphabet” is . . . | → | Characters | Tokens |
| A “string” is . . . | → | Lexeme or token | Expression |
| It’s implemented by the . . . | → | Scanner | Parser |
Nhiệm vụ của một ngữ pháp hình thức là xác định chuỗi nào là hợp lệ và chuỗi nào thì không. Nếu ta đang định nghĩa một ngữ pháp cho câu tiếng Anh, “eggs are tasty for breakfast” sẽ thuộc ngữ pháp, nhưng “tasty breakfast for are eggs” thì có lẽ không.
5 . 1 . 1Quy tắc cho ngữ pháp
Làm sao để ta viết ra một ngữ pháp chứa vô hạn chuỗi hợp lệ? Rõ ràng ta không thể liệt kê hết tất cả. Thay vào đó, ta tạo ra một tập hữu hạn các quy tắc. Bạn có thể hình dung chúng như một trò chơi mà bạn có thể “chơi” theo một trong hai hướng.
Nếu bắt đầu từ các quy tắc, bạn có thể dùng chúng để tạo ra các chuỗi thuộc ngữ pháp. Các chuỗi được tạo theo cách này được gọi là derivation vì mỗi chuỗi được suy ra từ các quy tắc của ngữ pháp. Ở mỗi bước của trò chơi, bạn chọn một quy tắc và làm theo những gì nó yêu cầu. Phần lớn thuật ngữ xoay quanh ngữ pháp hình thức xuất phát từ cách “chơi” này. Các quy tắc được gọi là production vì chúng sinh ra các chuỗi trong ngữ pháp.
Mỗi production trong một ngữ pháp phi ngữ cảnh có một head — tên của nó — và một body, mô tả những gì nó sinh ra. Ở dạng thuần túy, body chỉ đơn giản là một danh sách các ký hiệu. Các ký hiệu này có hai “hương vị” hấp dẫn:
-
Terminal là một ký tự trong bảng chữ cái của ngữ pháp. Bạn có thể coi nó như một giá trị literal. Trong ngữ pháp cú pháp mà ta đang định nghĩa, các terminal là những lexeme riêng lẻ — các token đến từ scanner như
ifhoặc1234.Chúng được gọi là “terminal” theo nghĩa “điểm kết thúc” vì chúng không dẫn đến bất kỳ “nước đi” nào khác trong trò chơi. Bạn chỉ đơn giản sinh ra ký hiệu đó.
-
Nonterminal là một tham chiếu có tên tới một quy tắc khác trong ngữ pháp. Nó có nghĩa là “chơi” quy tắc đó và chèn bất cứ thứ gì nó sinh ra vào đây. Theo cách này, ngữ pháp được ghép thành.
Có một tinh chỉnh cuối cùng: bạn có thể có nhiều quy tắc cùng tên. Khi gặp một nonterminal với tên đó, bạn được phép chọn bất kỳ quy tắc nào trong số đó, tùy ý bạn.
Để cụ thể hơn, ta cần một cách để viết ra các production rule này. Con người đã cố gắng “kết tinh” ngữ pháp từ thời Ashtadhyayi của Pāṇini, bộ sách đã hệ thống hóa ngữ pháp tiếng Phạn cách đây chỉ vài nghìn năm. Không có nhiều tiến triển cho đến khi John Backus và cộng sự cần một ký hiệu để đặc tả ALGOL 58 và nghĩ ra Backus-Naur form (BNF). Kể từ đó, gần như ai cũng dùng một biến thể nào đó của BNF, được chỉnh sửa theo sở thích riêng.
Tôi đã cố gắng nghĩ ra một dạng ký hiệu gọn gàng. Mỗi quy tắc gồm một tên, theo sau là một mũi tên (→), tiếp đến là một chuỗi ký hiệu, và kết thúc bằng dấu chấm phẩy (;). Terminal là các chuỗi được đặt trong dấu nháy, còn nonterminal là các từ viết thường.
Dùng cách này, đây là một ngữ pháp cho thực đơn bữa sáng:
breakfast → protein "with" breakfast "on the side" ; breakfast → protein ; breakfast → bread ; protein → crispiness "crispy" "bacon" ; protein → "sausage" ; protein → cooked "eggs" ; crispiness → "really" ; crispiness → "really" crispiness ; cooked → "scrambled" ; cooked → "poached" ; cooked → "fried" ; bread → "toast" ; bread → "biscuits" ; bread → "English muffin" ;
Ta có thể dùng ngữ pháp này để tạo ra các bữa sáng ngẫu nhiên. Hãy “chơi” một ván để xem nó hoạt động thế nào. Theo thông lệ lâu đời, trò chơi bắt đầu với quy tắc đầu tiên trong ngữ pháp, ở đây là breakfast. Có ba production cho quy tắc này, và ta ngẫu nhiên chọn cái đầu tiên. Chuỗi kết quả của ta trông như sau:
protein "with" breakfast "on the side"
Ta cần mở rộng nonterminal đầu tiên, protein, nên ta chọn một production cho nó. Chọn:
protein → cooked "eggs" ;
Tiếp theo, ta cần một production cho cooked, và ta chọn "poached". Đây là một terminal, nên ta thêm nó vào. Giờ chuỗi của ta trông như:
"poached" "eggs" "with" breakfast "on the side"
Nonterminal tiếp theo lại là breakfast. Production breakfast đầu tiên mà ta chọn tham chiếu đệ quy trở lại quy tắc breakfast. Sự xuất hiện của đệ quy trong ngữ pháp là một dấu hiệu tốt cho thấy ngôn ngữ đang được định nghĩa là phi ngữ cảnh (context-free) thay vì chính quy (regular). Đặc biệt, đệ quy mà nonterminal đệ quy có production ở cả hai phía cho thấy ngôn ngữ đó không phải là chính quy.
Ta có thể cứ chọn production đầu tiên cho breakfast lặp đi lặp lại, tạo ra đủ loại bữa sáng như “bacon with sausage with scrambled eggs with bacon…”. Nhưng ta sẽ không làm vậy. Lần này ta sẽ chọn bread. Có ba quy tắc cho nó, mỗi quy tắc chỉ chứa một terminal. Ta sẽ chọn “English muffin”.
Với lựa chọn đó, mọi nonterminal trong chuỗi đã được mở rộng cho đến khi cuối cùng chỉ còn lại các terminal và ta thu được:
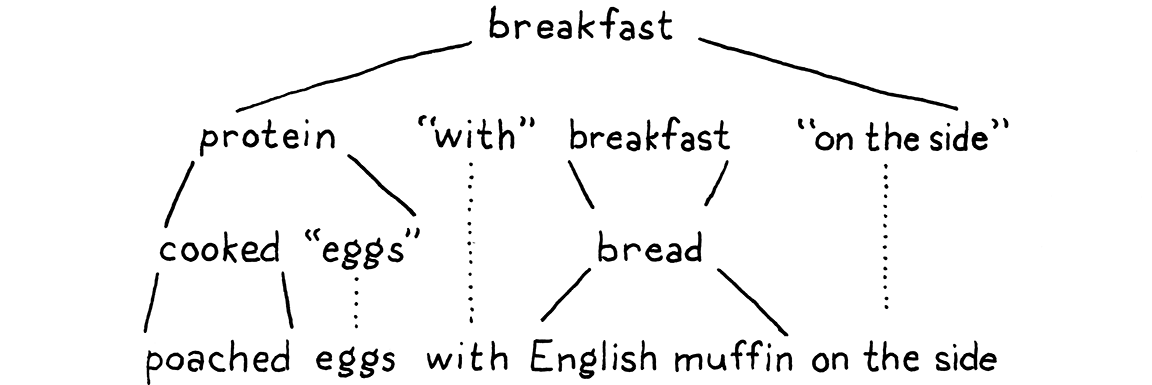
Thêm chút thịt nguội và sốt Hollandaise, bạn sẽ có món eggs Benedict.
Bất cứ khi nào ta gặp một quy tắc có nhiều production, ta chỉ việc chọn một cái bất kỳ. Chính sự linh hoạt này cho phép một số lượng nhỏ quy tắc ngữ pháp mã hóa được một tập hợp chuỗi lớn hơn theo cấp số nhân. Việc một quy tắc có thể tham chiếu tới chính nó — trực tiếp hoặc gián tiếp — còn nâng tầm hơn nữa, cho phép ta “nhét” một số lượng vô hạn chuỗi vào một ngữ pháp hữu hạn.
5 . 1 . 2Nâng cấp ký pháp của chúng ta
Nhét một tập hợp vô hạn chuỗi vào chỉ vài quy tắc là khá tuyệt, nhưng hãy tiến xa hơn. Ký pháp của ta hoạt động, nhưng hơi tẻ nhạt. Vậy nên, như bất kỳ nhà thiết kế ngôn ngữ giỏi nào, ta sẽ rắc thêm chút “đường cú pháp” — một vài ký pháp tiện lợi bổ sung. Ngoài terminal và nonterminal, ta sẽ cho phép một vài loại biểu thức khác trong phần thân của quy tắc:
-
Thay vì lặp lại tên quy tắc mỗi khi muốn thêm một production mới cho nó, ta sẽ cho phép một chuỗi các production được phân tách bằng dấu gạch đứng (
|).bread → "toast" | "biscuits" | "English muffin" ;
-
Hơn nữa, ta sẽ cho phép dấu ngoặc đơn để nhóm, và cho phép
|bên trong đó để chọn một trong nhiều tùy chọn ở giữa một production.protein → ( "scrambled" | "poached" | "fried" ) "eggs" ;
-
Dùng đệ quy để hỗ trợ chuỗi ký hiệu lặp lại có một nét “thuần khiết” nhất định, nhưng khá mất công khi phải tạo một quy tắc con đặt tên riêng mỗi khi muốn lặp. Vì vậy, ta cũng dùng hậu tố
*để cho phép ký hiệu hoặc nhóm trước đó lặp lại từ 0 lần trở lên.crispiness → "really" "really"* ;
-
Hậu tố
+tương tự như vậy, nhưng yêu cầu production đứng trước nó phải xuất hiện ít nhất một lần.crispiness → "really"+ ;
-
Hậu tố
?dùng cho một production tùy chọn. Thành phần đứng trước nó có thể xuất hiện 0 hoặc 1 lần, nhưng không hơn.breakfast → protein ( "with" breakfast "on the side" )? ;
Với tất cả những “đường cú pháp” này, ngữ pháp bữa sáng của ta được rút gọn thành:
breakfast → protein ( "with" breakfast "on the side" )? | bread ; protein → "really"+ "crispy" "bacon" | "sausage" | ( "scrambled" | "poached" | "fried" ) "eggs" ; bread → "toast" | "biscuits" | "English muffin" ;
Cũng không tệ lắm, nhỉ. Nếu bạn quen dùng grep hoặc regular expressions trong trình soạn thảo văn bản, hầu hết các ký hiệu này sẽ khá quen thuộc. Khác biệt chính là ở đây, các ký hiệu đại diện cho cả một token, chứ không phải một ký tự đơn lẻ.
Ta sẽ dùng ký pháp này xuyên suốt phần còn lại của cuốn sách để mô tả chính xác ngữ pháp của Lox. Khi bạn làm việc với ngôn ngữ lập trình, bạn sẽ thấy rằng ngữ pháp phi ngữ cảnh (dùng ký pháp này, hoặc EBNF, hoặc ký pháp khác) giúp bạn “kết tinh” các ý tưởng thiết kế cú pháp còn mơ hồ. Chúng cũng là một phương tiện hữu ích để trao đổi với những người “vọc” ngôn ngữ khác về cú pháp.
Các quy tắc và production mà ta định nghĩa cho Lox cũng sẽ là kim chỉ nam cho cấu trúc dữ liệu dạng cây mà ta sẽ hiện thực để biểu diễn code trong bộ nhớ. Trước khi làm điều đó, ta cần một ngữ pháp thực sự cho Lox, hoặc ít nhất là đủ để bắt đầu.
5 . 1 . 3Ngữ pháp cho các biểu thức Lox
Trong chương trước, ta đã hoàn thành toàn bộ ngữ pháp từ vựng của Lox trong một lần. Mọi từ khóa và ký hiệu đều đã có. Ngữ pháp cú pháp thì lớn hơn, và sẽ thật nhàm chán nếu phải cày qua toàn bộ trước khi interpreter của ta chạy được.
Thay vào đó, trong vài chương tới, ta sẽ xử lý một tập con của ngôn ngữ. Khi ta đã biểu diễn, parse và chạy được mini-language này, các chương sau sẽ dần dần bổ sung thêm tính năng mới, bao gồm cú pháp mới. Hiện tại, ta chỉ quan tâm đến một vài loại biểu thức:
-
Literal. Số, chuỗi, Boolean và
nil. -
Unary expression. Toán tử tiền tố
!để phủ định logic, và-để đổi dấu số. -
Binary expression. Các toán tử số học trung tố (
+,-,*,/) và toán tử logic (==,!=,<,<=,>,>=) quen thuộc. -
Ngoặc đơn. Một cặp
(và)bao quanh một biểu thức.
Như vậy là đủ cú pháp để viết các biểu thức như:
1 - (2 * 3) < 4 == false
Dùng ký pháp mới tiện lợi này, đây là ngữ pháp cho các biểu thức đó:
expression → literal | unary | binary | grouping ; literal → NUMBER | STRING | "true" | "false" | "nil" ; grouping → "(" expression ")" ; unary → ( "-" | "!" ) expression ; binary → expression operator expression ; operator → "==" | "!=" | "<" | "<=" | ">" | ">=" | "+" | "-" | "*" | "/" ;
Có một chút metasyntax bổ sung ở đây. Ngoài các chuỗi đặt trong dấu nháy cho terminal khớp chính xác với lexeme, ta viết HOA các terminal là một lexeme duy nhất nhưng phần văn bản có thể thay đổi. NUMBER là bất kỳ literal số nào, và STRING là bất kỳ literal chuỗi nào. Sau này, ta sẽ làm tương tự với IDENTIFIER.
Ngữ pháp này thực ra là mơ hồ, điều mà ta sẽ thấy khi parse nó. Nhưng hiện tại, như vậy là đủ.
5 . 2Hiện thực Syntax Tree
Cuối cùng thì ta cũng được viết code. Ngữ pháp biểu thức nhỏ kia chính là bộ khung của ta. Vì ngữ pháp này là đệ quy — để ý xem grouping, unary và binary đều tham chiếu ngược lại expression — nên cấu trúc dữ liệu của ta sẽ tạo thành một cây. Vì cấu trúc này biểu diễn cú pháp của ngôn ngữ, nó được gọi là syntax tree.
Scanner của ta dùng một class Token duy nhất để biểu diễn mọi loại lexeme. Để phân biệt các loại khác nhau — ví dụ số 123 so với chuỗi "123" — ta dùng một enum TokenType đơn giản. Syntax tree thì không đồng nhất như vậy. Biểu thức unary có một toán hạng, binary có hai, còn literal thì không có toán hạng nào.
Ta có thể nhồi tất cả vào một class Expression duy nhất với một danh sách con tùy ý. Một số compiler làm vậy. Nhưng tôi muốn tận dụng tối đa hệ thống kiểu của Java. Vậy nên ta sẽ định nghĩa một class cơ sở cho các biểu thức. Sau đó, với mỗi loại biểu thức — mỗi production dưới expression — ta tạo một subclass có các field cho các nonterminal đặc thù của quy tắc đó. Cách này giúp ta nhận lỗi biên dịch nếu, chẳng hạn, cố truy cập toán hạng thứ hai của một biểu thức unary.
Ví dụ như thế này:
package com.craftinginterpreters.lox; abstract class Expr { static class Binary extends Expr { Binary(Expr left, Token operator, Expr right) { this.left = left; this.operator = operator; this.right = right; } final Expr left; final Token operator; final Expr right; } // Other expressions... }
Expr là class cơ sở mà tất cả các class biểu thức kế thừa. Như bạn thấy ở Binary, các subclass được lồng bên trong nó. Không có lý do kỹ thuật bắt buộc, nhưng cách này cho phép ta nhét tất cả class vào một file Java duy nhất.
5 . 2 . 1Những object “mất phương hướng”
Bạn sẽ thấy rằng, giống như class Token, ở đây không có method nào cả. Đây là một cấu trúc “ngu ngốc”. Kiểu dữ liệu rõ ràng, nhưng chỉ là một túi dữ liệu. Điều này nghe có vẻ lạ trong một ngôn ngữ hướng đối tượng như Java. Chẳng phải class nên làm gì đó sao?
Vấn đề là các class cây này không thuộc về một miền (domain) cụ thể nào. Chúng có nên có method để parse vì đó là nơi chúng được tạo ra? Hay method để interpret vì đó là nơi chúng được sử dụng? Cây trải dài qua ranh giới giữa hai “lãnh thổ” đó, nghĩa là thực ra chúng không thuộc hẳn về bên nào.
Thực tế, các kiểu dữ liệu này tồn tại để cho parser và interpreter giao tiếp với nhau. Điều đó dẫn đến các kiểu dữ liệu chỉ đơn thuần chứa dữ liệu, không có hành vi đi kèm. Phong cách này rất tự nhiên trong các ngôn ngữ lập trình hàm như Lisp và ML, nơi mọi dữ liệu đều tách biệt với hành vi, nhưng trong Java thì cảm giác hơi lạ.
Những người yêu lập trình hàm lúc này hẳn đang nhảy lên và nói “Thấy chưa! Ngôn ngữ hướng đối tượng không hợp để viết interpreter!”. Tôi thì không đi xa đến vậy. Bạn còn nhớ scanner của ta rất hợp với hướng đối tượng chứ. Nó có đầy đủ trạng thái thay đổi để theo dõi vị trí trong source code, một tập hợp method public rõ ràng, và một vài helper private.
Cảm nhận của tôi là mỗi giai đoạn hoặc phần của interpreter đều hoạt động tốt với phong cách hướng đối tượng. Chỉ là các cấu trúc dữ liệu truyền giữa chúng thì bị “tước” hết hành vi mà thôi.
5 . 2 . 2Metaprogramming cho cây
Java có thể biểu diễn các class không có hành vi, nhưng tôi sẽ không nói rằng nó làm việc đó một cách đặc biệt tốt. Viết 11 dòng code chỉ để nhét ba field vào một object thì khá là tẻ nhạt, và khi xong xuôi, chúng ta sẽ có tới 21 class kiểu này.
Tôi không muốn lãng phí thời gian của bạn hay mực của tôi để viết hết đống đó. Thực ra, bản chất của mỗi subclass là gì? Một cái tên, và một danh sách các field có kiểu. Hết. Chúng ta là những kẻ “vọc” ngôn ngữ thông minh, đúng không? Hãy tự động hóa thôi.
Thay vì cặm cụi viết tay từng định nghĩa class, khai báo field, constructor và initializer, ta sẽ “chế” một script để làm việc đó cho mình. Script này chứa mô tả của từng loại cây — tên và các field — và in ra code Java cần thiết để định nghĩa một class với tên và trạng thái đó.
Script này là một ứng dụng Java dòng lệnh nhỏ, tạo ra một file tên là Expr.java:
create new file
package com.craftinginterpreters.tool; import java.io.IOException; import java.io.PrintWriter; import java.util.Arrays; import java.util.List; public class GenerateAst { public static void main(String[] args) throws IOException { if (args.length != 1) { System.err.println("Usage: generate_ast <output directory>"); System.exit(64); } String outputDir = args[0]; } }
Lưu ý rằng file này nằm trong một package khác, .tool thay vì .lox. Script này không phải là một phần của interpreter. Đây là công cụ mà chúng ta, những người đang “vọc” interpreter, tự chạy để sinh ra các class syntax tree. Khi xong, ta coi Expr.java như bất kỳ file nào khác trong phần hiện thực. Ta chỉ đơn giản là tự động hóa cách file đó được tạo ra.
Để sinh ra các class, nó cần có mô tả của từng loại và các field của chúng.
String outputDir = args[0];
in main()
defineAst(outputDir, "Expr", Arrays.asList( "Binary : Expr left, Token operator, Expr right", "Grouping : Expr expression", "Literal : Object value", "Unary : Token operator, Expr right" ));
}
Để ngắn gọn, tôi nhét mô tả các loại biểu thức vào trong chuỗi. Mỗi chuỗi là tên class, theo sau là : và danh sách các field, phân tách bằng dấu phẩy. Mỗi field có một kiểu và một tên.
Việc đầu tiên defineAst() cần làm là xuất ra class cơ sở Expr.
add after main()
private static void defineAst( String outputDir, String baseName, List<String> types) throws IOException { String path = outputDir + "/" + baseName + ".java"; PrintWriter writer = new PrintWriter(path, "UTF-8"); writer.println("package com.craftinginterpreters.lox;"); writer.println(); writer.println("import java.util.List;"); writer.println(); writer.println("abstract class " + baseName + " {"); writer.println("}"); writer.close(); }
Khi ta gọi hàm này, baseName là "Expr", vừa là tên class vừa là tên file được xuất ra. Ta truyền nó như một tham số thay vì hardcode tên, vì sau này ta sẽ thêm một nhóm class riêng cho statement.
Bên trong class cơ sở, ta định nghĩa từng subclass.
writer.println("abstract class " + baseName + " {");
in defineAst()
// The AST classes. for (String type : types) { String className = type.split(":")[0].trim(); String fields = type.split(":")[1].trim(); defineType(writer, baseName, className, fields); }
writer.println("}");
Đoạn code đó lại gọi tới:
add after defineAst()
private static void defineType( PrintWriter writer, String baseName, String className, String fieldList) { writer.println(" static class " + className + " extends " + baseName + " {"); // Constructor. writer.println(" " + className + "(" + fieldList + ") {"); // Store parameters in fields. String[] fields = fieldList.split(", "); for (String field : fields) { String name = field.split(" ")[1]; writer.println(" this." + name + " = " + name + ";"); } writer.println(" }"); // Fields. writer.println(); for (String field : fields) { writer.println(" final " + field + ";"); } writer.println(" }"); }
Vậy là xong. Tất cả phần Java boilerplate “huy hoàng” đó đã được xử lý. Nó khai báo từng field trong thân class. Nó định nghĩa constructor cho class với các tham số tương ứng với từng field và khởi tạo chúng trong thân hàm.
Biên dịch và chạy chương trình Java này ngay bây giờ và nó sẽ “bắn” ra một file .java mới chứa vài chục dòng code. File đó sẽ còn dài hơn nữa.
5 . 3Làm việc với cây
Hãy đội chiếc “mũ tưởng tượng” của bạn lên một chút. Dù ta chưa đến bước đó, hãy thử hình dung interpreter sẽ làm gì với các syntax tree. Mỗi loại biểu thức trong Lox có hành vi khác nhau khi chạy. Điều đó có nghĩa là interpreter cần chọn một đoạn code khác nhau để xử lý từng loại biểu thức. Với token, ta chỉ cần switch trên TokenType. Nhưng với syntax tree, ta không có một enum “type” nào, mà chỉ có mỗi loại là một class Java riêng.
Ta có thể viết một chuỗi dài các phép kiểm tra kiểu:
if (expr instanceof Expr.Binary) { // ... } else if (expr instanceof Expr.Grouping) { // ... } else // ...
Nhưng tất cả các phép kiểm tra tuần tự này đều chậm. Các loại biểu thức có tên đứng sau trong bảng chữ cái sẽ mất nhiều thời gian hơn để execute vì chúng phải “rơi” qua nhiều nhánh if hơn trước khi tìm đúng loại. Đây không phải là giải pháp “thanh lịch” mà tôi muốn.
Ta có một “gia đình” các class và cần gắn một đoạn hành vi với mỗi class. Giải pháp tự nhiên trong một ngôn ngữ hướng đối tượng như Java là đặt các hành vi đó vào các method ngay trong class. Ta có thể thêm một method trừu tượng interpret() vào Expr, và mỗi subclass sẽ tự hiện thực nó để tự diễn giải chính nó.
Cách này ổn với các dự án nhỏ, nhưng mở rộng kém. Như tôi đã nói trước đó, các class cây này trải qua nhiều “miền” khác nhau. Ít nhất thì cả parser và interpreter đều sẽ “đụng” vào chúng. Như bạn sẽ thấy sau này, ta cần thực hiện name resolution trên chúng. Nếu ngôn ngữ của ta là kiểu tĩnh, ta sẽ có thêm một bước kiểm tra kiểu.
Nếu ta thêm method instance vào các class biểu thức cho từng thao tác như vậy, ta sẽ trộn lẫn nhiều miền khác nhau vào cùng một chỗ. Điều đó vi phạm nguyên tắc separation of concerns và dẫn đến code khó bảo trì.
5 . 3 . 1Vấn đề “expression problem”
Vấn đề này thực ra cơ bản hơn bạn tưởng. Ta có một số loại (type), và một số thao tác cấp cao như “interpret”. Với mỗi cặp loại và thao tác, ta cần một hiện thực cụ thể. Hãy hình dung một bảng:
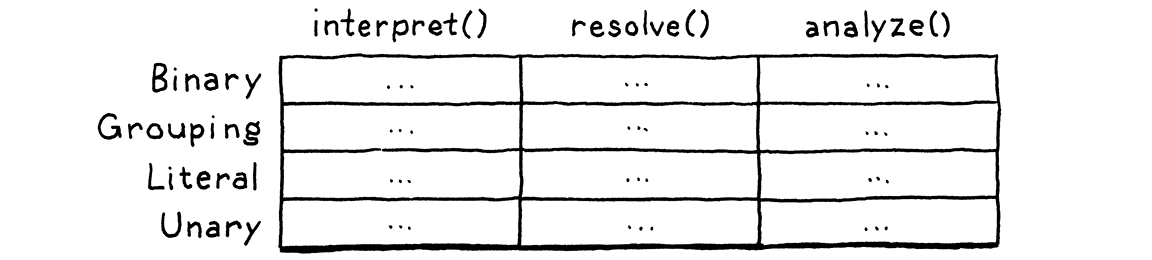
Các hàng là type, và các cột là thao tác. Mỗi ô biểu diễn một đoạn code duy nhất để hiện thực thao tác đó trên type đó.
Một ngôn ngữ hướng đối tượng như Java giả định rằng tất cả code trong một hàng tự nhiên thuộc về nhau. Nó cho rằng mọi thứ bạn làm với một type có liên quan đến nhau, và ngôn ngữ giúp bạn dễ dàng định nghĩa chúng cùng nhau dưới dạng method trong cùng một class.
Điều này giúp dễ dàng mở rộng bảng bằng cách thêm hàng mới. Chỉ cần định nghĩa một class mới. Không cần chạm vào code hiện có. Nhưng hãy tưởng tượng nếu bạn muốn thêm một thao tác mới — một cột mới. Trong Java, điều đó có nghĩa là phải mở từng class hiện có và thêm một method vào đó.
Các ngôn ngữ thuộc họ lập trình hàm ML thì đảo ngược điều này. Ở đó, bạn không có class với method. Type và function hoàn toàn tách biệt. Để hiện thực một thao tác cho nhiều type khác nhau, bạn định nghĩa một hàm duy nhất. Trong thân hàm đó, bạn dùng pattern matching — kiểu như một switch dựa trên type nhưng “nâng cấp” — để hiện thực thao tác cho từng type ngay tại một chỗ.
Cách này giúp việc thêm thao tác mới trở nên đơn giản — chỉ cần định nghĩa thêm một hàm khác, pattern match trên tất cả các type.
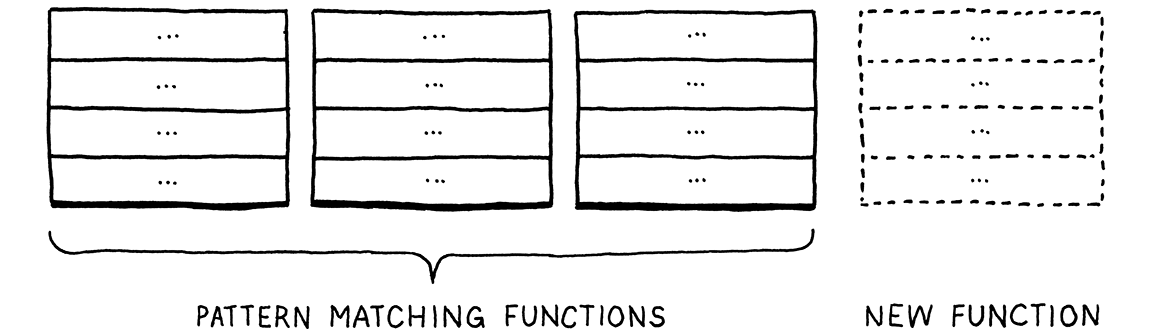
Nhưng ngược lại, việc thêm một type mới lại khó. Bạn phải quay lại và thêm một case mới vào tất cả các pattern match trong mọi hàm hiện có.
Mỗi phong cách lập trình đều có một “thớ” riêng. Đó cũng chính là ý nghĩa của tên gọi paradigm — một ngôn ngữ hướng đối tượng muốn bạn định hướng code của mình theo các hàng (row) là các type. Ngôn ngữ lập trình hàm thì khuyến khích bạn gom toàn bộ code của mỗi cột thành một hàm.
Một nhóm “mọt” ngôn ngữ thông minh đã nhận ra rằng không phong cách nào giúp việc thêm cả hàng và cột vào bảng trở nên dễ dàng. Họ gọi khó khăn này là “expression problem” vì — giống như chúng ta bây giờ — họ lần đầu gặp nó khi tìm cách mô hình hóa các node syntax tree của biểu thức trong một compiler.
Người ta đã thử đủ loại tính năng ngôn ngữ, design pattern và mẹo lập trình để giải quyết vấn đề này, nhưng chưa có ngôn ngữ “hoàn hảo” nào xử lý triệt để. Trong lúc chờ đợi, điều tốt nhất ta có thể làm là chọn một ngôn ngữ có “thớ” phù hợp với các đường ranh kiến trúc tự nhiên trong chương trình ta đang viết.
Hướng đối tượng hoạt động tốt với nhiều phần của interpreter, nhưng các class cây này lại “ngược thớ” với Java. May mắn thay, có một design pattern mà ta có thể áp dụng.
5 . 3 . 2Visitor pattern
Visitor pattern là pattern bị hiểu nhầm nhiều nhất trong toàn bộ Design Patterns, và điều đó thực sự nói lên nhiều điều nếu bạn nhìn vào những “thái quá” trong kiến trúc phần mềm vài thập kỷ qua.
Rắc rối bắt đầu từ thuật ngữ. Pattern này không liên quan gì đến “thăm viếng”, và method accept trong đó cũng chẳng gợi ra hình ảnh gì hữu ích. Nhiều người nghĩ pattern này liên quan đến việc duyệt cây, nhưng thực ra không phải. Chúng ta sẽ dùng nó trên một tập các class có dạng cây, nhưng đó chỉ là sự trùng hợp. Như bạn sẽ thấy, pattern này hoạt động tốt ngay cả trên một object đơn lẻ.
Thực chất, Visitor pattern là cách “mô phỏng” phong cách lập trình hàm trong một ngôn ngữ OOP. Nó cho phép ta dễ dàng thêm các cột mới vào bảng. Ta có thể định nghĩa toàn bộ hành vi cho một thao tác mới trên một tập type ở cùng một chỗ, mà không cần chạm vào chính các type đó. Nó làm điều này theo cách mà ta giải quyết hầu hết mọi vấn đề trong khoa học máy tính: thêm một lớp gián tiếp.
Trước khi áp dụng nó vào các class Expr sinh tự động, hãy cùng đi qua một ví dụ đơn giản hơn. Giả sử ta có hai loại bánh ngọt: beignet và cruller.
abstract class Pastry { } class Beignet extends Pastry { } class Cruller extends Pastry { }
Ta muốn có thể định nghĩa các thao tác mới với bánh ngọt — nấu, ăn, trang trí, v.v. — mà không phải thêm method mới vào từng class mỗi lần. Đây là cách làm. Đầu tiên, ta định nghĩa một interface riêng.
interface PastryVisitor { void visitBeignet(Beignet beignet); void visitCruller(Cruller cruller); }
Mỗi thao tác có thể thực hiện trên bánh ngọt là một class mới implement interface đó. Nó có một method cụ thể cho từng loại bánh. Điều này giữ cho code của thao tác trên cả hai loại được gói gọn trong một class.
Khi có một chiếc bánh, làm sao ta điều hướng nó tới đúng method trên visitor dựa trên type của nó? Câu trả lời là: nhờ polymorphism! Ta thêm method này vào Pastry:
abstract class Pastry {
abstract void accept(PastryVisitor visitor);
}
Mỗi subclass sẽ hiện thực nó.
class Beignet extends Pastry {
@Override void accept(PastryVisitor visitor) { visitor.visitBeignet(this); }
}
Và:
class Cruller extends Pastry {
@Override void accept(PastryVisitor visitor) { visitor.visitCruller(this); }
}
Để thực hiện một thao tác trên bánh, ta gọi method accept() của nó và truyền vào visitor cho thao tác muốn thực hiện. Chiếc bánh — cụ thể là hiện thực override accept() của subclass — sẽ gọi ngược lại method visit phù hợp trên visitor và truyền chính nó vào.
Đó chính là mấu chốt của “mẹo” này. Nó cho phép ta dùng polymorphic dispatch trên các class bánh để chọn method phù hợp trên class visitor. Trong bảng, mỗi class bánh là một hàng, nhưng nếu bạn nhìn vào tất cả các method của một visitor, chúng tạo thành một cột.
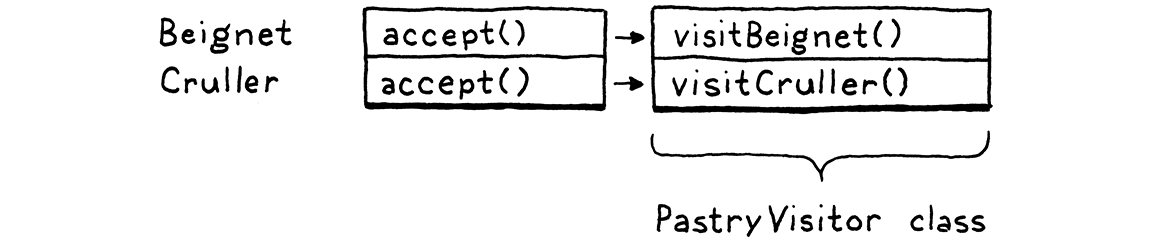
Chúng ta đã thêm một phương thức accept() vào mỗi class, và có thể dùng nó cho bao nhiêu visitor tùy thích mà không bao giờ phải đụng lại vào các class bánh ngọt nữa. Đây là một pattern khá thông minh.
5 . 3 . 3Visitor cho biểu thức
Được rồi, hãy đưa nó vào các class biểu thức của chúng ta. Ta cũng sẽ tinh chỉnh pattern này một chút. Trong ví dụ bánh ngọt, các phương thức visit và accept() không trả về gì cả. Trên thực tế, visitor thường muốn định nghĩa các thao tác tạo ra giá trị. Nhưng accept() nên có kiểu trả về gì? Ta không thể giả định mọi class visitor đều muốn trả về cùng một kiểu, nên ta sẽ dùng generics để cho phép mỗi hiện thực tự chỉ định kiểu trả về.
Trước tiên, ta định nghĩa interface visitor. Một lần nữa, ta lồng nó bên trong class cơ sở để giữ mọi thứ trong một file.
writer.println("abstract class " + baseName + " {");
in defineAst()
defineVisitor(writer, baseName, types);
// The AST classes.
Hàm này sinh ra interface visitor.
add after defineAst()
private static void defineVisitor( PrintWriter writer, String baseName, List<String> types) { writer.println(" interface Visitor<R> {"); for (String type : types) { String typeName = type.split(":")[0].trim(); writer.println(" R visit" + typeName + baseName + "(" + typeName + " " + baseName.toLowerCase() + ");"); } writer.println(" }"); }
Ở đây, ta duyệt qua tất cả các subclass và khai báo một phương thức visit cho từng cái. Khi ta định nghĩa các loại biểu thức mới sau này, chúng sẽ tự động được thêm vào.
Bên trong class cơ sở, ta định nghĩa phương thức trừu tượng accept().
defineType(writer, baseName, className, fields);
}
in defineAst()
// The base accept() method.
writer.println();
writer.println(" abstract <R> R accept(Visitor<R> visitor);");
writer.println("}");
Cuối cùng, mỗi subclass sẽ hiện thực phương thức đó và gọi đúng phương thức visit cho loại của chính nó.
writer.println(" }");
in defineType()
// Visitor pattern.
writer.println();
writer.println(" @Override");
writer.println(" <R> R accept(Visitor<R> visitor) {");
writer.println(" return visitor.visit" +
className + baseName + "(this);");
writer.println(" }");
// Fields.
Vậy là xong. Giờ ta có thể định nghĩa các thao tác trên biểu thức mà không cần phải chỉnh sửa các class hay script sinh code. Hãy biên dịch và chạy script sinh code này để xuất ra file Expr.java đã được cập nhật. Nó chứa một interface Visitor được generated và một tập các class node biểu thức hỗ trợ Visitor pattern.
Trước khi kết thúc chương dài dòng này, hãy hiện thực interface Visitor đó và xem pattern này hoạt động ra sao.
5 . 4Một bộ in (không mấy) đẹp
Khi debug parser và interpreter, việc nhìn vào một syntax tree đã parse và đảm bảo nó có cấu trúc như mong đợi thường rất hữu ích. Ta có thể kiểm tra nó trong debugger, nhưng việc đó khá mất công.
Thay vào đó, ta muốn có một đoạn code mà, khi nhận vào một syntax tree, sẽ tạo ra một chuỗi biểu diễn rõ ràng, không mơ hồ của nó. Việc chuyển một cây thành chuỗi có thể coi là ngược lại với parser, và thường được gọi là “pretty printing” khi mục tiêu là tạo ra một chuỗi văn bản có cú pháp hợp lệ trong ngôn ngữ nguồn.
Nhưng đó không phải mục tiêu của ta ở đây. Ta muốn chuỗi này thể hiện thật rõ ràng cấu trúc lồng nhau của cây. Một bộ in trả về 1 + 2 * 3 sẽ không hữu ích lắm nếu điều ta đang cố debug là việc xử lý precedence của toán tử có đúng không. Ta muốn biết + hay * nằm ở đỉnh của cây.
Vì vậy, chuỗi mà ta tạo ra sẽ không phải cú pháp Lox. Thay vào đó, nó sẽ trông khá giống Lisp. Mỗi biểu thức được đặt trong ngoặc đơn một cách tường minh, và tất cả các biểu thức con cùng token của nó đều nằm bên trong.
Với một syntax tree như:
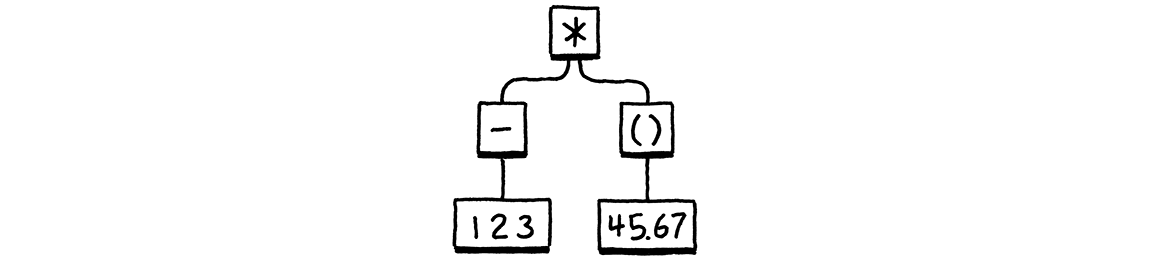
Nó sẽ tạo ra:
(* (- 123) (group 45.67))
Không hẳn là “đẹp”, nhưng nó thể hiện rõ ràng sự lồng ghép và nhóm biểu thức. Để hiện thực điều này, ta định nghĩa một class mới.
create new file
package com.craftinginterpreters.lox; class AstPrinter implements Expr.Visitor<String> { String print(Expr expr) { return expr.accept(this); } }
Như bạn thấy, nó hiện thực interface visitor. Điều đó có nghĩa là ta cần các phương thức visit cho từng loại biểu thức hiện có.
return expr.accept(this); }
add after print()
@Override public String visitBinaryExpr(Expr.Binary expr) { return parenthesize(expr.operator.lexeme, expr.left, expr.right); } @Override public String visitGroupingExpr(Expr.Grouping expr) { return parenthesize("group", expr.expression); } @Override public String visitLiteralExpr(Expr.Literal expr) { if (expr.value == null) return "nil"; return expr.value.toString(); } @Override public String visitUnaryExpr(Expr.Unary expr) { return parenthesize(expr.operator.lexeme, expr.right); }
}
Biểu thức literal thì dễ — chỉ cần chuyển giá trị thành chuỗi, kèm một chút kiểm tra để xử lý null của Java thay cho nil của Lox. Các biểu thức khác có biểu thức con, nên chúng dùng phương thức tiện ích parenthesize() này:
add after visitUnaryExpr()
private String parenthesize(String name, Expr... exprs) { StringBuilder builder = new StringBuilder(); builder.append("(").append(name); for (Expr expr : exprs) { builder.append(" "); builder.append(expr.accept(this)); } builder.append(")"); return builder.toString(); }
Nó nhận một tên và một danh sách các biểu thức con, rồi bao tất cả trong ngoặc đơn, tạo ra một chuỗi như:
(+ 1 2)
Lưu ý rằng nó gọi accept() trên từng biểu thức con và truyền vào chính nó. Đây là bước đệ quy cho phép ta in ra toàn bộ cây.
Chúng ta chưa có parser, nên hơi khó để thấy pattern này hoạt động thế nào. Tạm thời, ta sẽ “chế” một phương thức main() nhỏ để tự tạo thủ công một cây và in nó ra.
add after parenthesize()
public static void main(String[] args) { Expr expression = new Expr.Binary( new Expr.Unary( new Token(TokenType.MINUS, "-", null, 1), new Expr.Literal(123)), new Token(TokenType.STAR, "*", null, 1), new Expr.Grouping( new Expr.Literal(45.67))); System.out.println(new AstPrinter().print(expression)); }
Nếu mọi thứ đúng, nó sẽ in ra:
(* (- 123) (group 45.67))
Bạn có thể xóa phương thức này đi. Ta sẽ không cần nó nữa. Ngoài ra, khi ta thêm các loại syntax tree mới, tôi sẽ không mất công hiển thị các phương thức visit cần thiết cho chúng trong AstPrinter. Nếu bạn muốn (và muốn Java compiler không “la” bạn), hãy tự thêm chúng vào. Điều này sẽ hữu ích trong chương sau khi ta bắt đầu parse code Lox thành syntax tree. Hoặc, nếu bạn không muốn duy trì AstPrinter, cứ thoải mái xóa nó. Ta sẽ không dùng lại nó nữa.
5 . 5Thử thách
-
Trước đó, tôi đã nói rằng các dạng
|,*và+mà ta thêm vào metasyntax của ngữ pháp chỉ là “đường cú pháp” (syntactic sugar). Hãy xem ngữ pháp này:expr → expr ( "(" ( expr ( "," expr )* )? ")" | "." IDENTIFIER )+ | IDENTIFIER | NUMBER
Hãy viết lại một ngữ pháp khớp cùng ngôn ngữ này nhưng không dùng bất kỳ “đường cú pháp” nào ở trên.
Bonus: Đoạn ngữ pháp này mô tả loại biểu thức gì?
-
Visitor pattern cho phép bạn mô phỏng phong cách lập trình hàm trong một ngôn ngữ hướng đối tượng. Hãy nghĩ ra một pattern bổ sung cho một ngôn ngữ lập trình hàm. Nó nên cho phép bạn gom tất cả các thao tác trên một type vào cùng một chỗ và cho phép định nghĩa type mới một cách dễ dàng.
(SML hoặc Haskell sẽ là lý tưởng cho bài tập này, nhưng Scheme hoặc một Lisp khác cũng được.)
-
Trong reverse Polish notation (RPN), các toán hạng của một toán tử số học đều được đặt trước toán tử, nên
1 + 2trở thành1 2 +. Việc tính toán diễn ra từ trái sang phải. Các số được đẩy vào một stack ngầm định. Một toán tử số học sẽ pop hai số trên cùng, thực hiện phép toán, rồi push kết quả trở lại. Do đó, biểu thức:(1 + 2) * (4 - 3)
trong RPN sẽ thành:
1 2 + 4 3 - *
Hãy định nghĩa một visitor class cho các syntax tree class của chúng ta, nhận vào một biểu thức, chuyển nó sang RPN và trả về chuỗi kết quả.