Matrices in Assembly - Đắm mình vào hệ thống

9.8. Ma trận (Matrices)

Ma trận là một mảng hai chiều (2D array).
Trong C, một ma trận có thể được:

Cấp phát tĩnh dưới dạng mảng 2D (M[n][m]) — nằm trên stack.
Cấp phát động bằng một lần gọi malloc.
Cấp phát động dưới dạng mảng của các mảng (array of arrays).

Hãy xét cách triển khai mảng của các mảng:
Mảng đầu tiên chứa n phần tử (M[n]), và mỗi phần tử M[i] lại chứa một mảng gồm m phần tử.

Ví dụ dưới đây khai báo các ma trận kích thước 4 × 3:

// ma trận cấp phát tĩnh (trên stack)
int M1[4][3];

// ma trận cấp phát động (dễ lập trình, trên heap)
int **M2, i;
M2 = malloc(4 * sizeof(int*));
for (i = 0; i < 4; i++) {
    M2[i] = malloc(3 * sizeof(int));
}

Với ma trận cấp phát động, mảng chính chứa một mảng liên tiếp các con trỏ int.
Mỗi con trỏ này trỏ tới một mảng khác trong bộ nhớ.

Hình 1 minh họa cách chúng ta thường hình dung hai loại ma trận này:

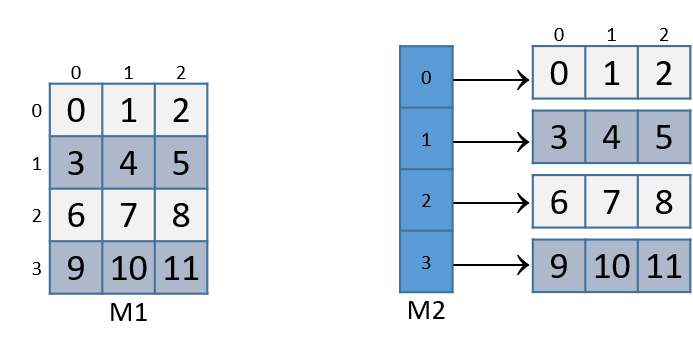
matrices

Hình 1. Minh họa ma trận cấp phát tĩnh (M1) và ma trận cấp phát động (M2) kích thước 3×4.

Với cả hai cách khai báo trên, phần tử (i, j) có thể được truy cập bằng cú pháp M[i][j], với M là M1 hoặc M2.
Tuy nhiên, cách tổ chức dữ liệu trong bộ nhớ là khác nhau:

Cả hai đều lưu các phần tử của mảng chính liên tiếp trong bộ nhớ.
Ma trận cấp phát tĩnh (M1) cũng lưu toàn bộ các hàng liên tiếp nhau trong bộ nhớ:

matrixArray

Hình 2. Bố trí bộ nhớ của M1 theo thứ tự hàng (row-major order).

Điều này không được đảm bảo với M2.
Nhớ rằng, để cấp phát liên tiếp một ma trận n × m trên heap, ta nên dùng một lần gọi malloc để cấp phát n × m phần tử:

// ma trận động (trên heap, cách hiệu quả về bộ nhớ)
#define ROWS 4
#define COLS 3
int *M3;
M3 = malloc(ROWS * COLS * sizeof(int));

Với khai báo M3, phần tử (i, j) không thể truy cập bằng cú pháp M[i][j].
Thay vào đó, phải truy cập bằng:

M3[i * cols + j]

9.8.1. Mảng hai chiều liên tiếp (Contiguous Two-Dimensional Arrays)

Xét hàm sumMat nhận:

Con trỏ tới một ma trận được cấp phát liên tiếp (tĩnh hoặc động hiệu quả bộ nhớ) làm tham số đầu tiên.
Số hàng và số cột.

Hàm trả về tổng tất cả các phần tử trong ma trận.

Ta dùng scaled indexing (chỉ số có nhân hệ số) vì nó áp dụng cho cả ma trận tĩnh và động liên tiếp.
Nhớ rằng cú pháp m[i][j] không hoạt động với cách cấp phát động liên tiếp hiệu quả bộ nhớ đã nói ở trên.

int sumMat(int *m, int rows, int cols) {
    int i, j, total = 0;
    for (i = 0; i < rows; i++) {
        for (j = 0; j < cols; j++) {
            total += m[i * cols + j];
        }
    }
    return total;
}

Dưới đây là code assembly tương ứng, với chú thích từng dòng:

Dump of assembler code for function sumMat:
0x884 <+0>:   sub   sp, sp, #0x20      // mở rộng stack thêm 32 byte (frame mới)
0x888 <+4>:   str   x0, [sp, #8]       // lưu m tại sp + 8
0x88c <+8>:   str   w1, [sp, #4]       // lưu rows tại sp + 4
0x890 <+12>:  str   w2, [sp]           // lưu cols tại đỉnh stack
0x894 <+16>:  str   wzr, [sp, #28]     // total = 0 tại sp + 28
0x898 <+20>:  str   wzr, [sp, #20]     // i = 0 tại sp + 20
0x89c <+24>:  b     0x904 <sumMat+128> // nhảy tới <sumMat+128>
0x8a0 <+28>:  str   wzr, [sp, #24]     // j = 0 tại sp + 24
0x8a4 <+32>:  b     0x8e8 <sumMat+100> // nhảy tới <sumMat+100>
0x8a8 <+36>:  ldr   w1, [sp, #20]      // w1 = i
0x8ac <+40>:  ldr   w0, [sp]           // w0 = cols
0x8b0 <+44>:  mul   w1, w1, w0         // w1 = cols * i
0x8b4 <+48>:  ldr   w0, [sp, #24]      // w0 = j
0x8b8 <+52>:  add   w0, w1, w0         // w0 = (cols * i) + j
0x8bc <+56>:  sxtw  x0, w0             // x0 = signExtend(cols * i + j)
0x8c0 <+60>:  lsl   x0, x0, #2         // x0 = (cols * i + j) * 4
0x8c4 <+64>:  ldr   x1, [sp, #8]       // x1 = m
0x8c8 <+68>:  add   x0, x1, x0         // x0 = &m[i*cols + j]
0x8cc <+72>:  ldr   w0, [x0]           // w0 = m[i*cols + j]
0x8d0 <+76>:  ldr   w1, [sp, #28]      // w1 = total
0x8d4 <+80>:  add   w0, w1, w0         // w0 = total + m[i*cols + j]
0x8d8 <+84>:  str   w0, [sp, #28]      // total = total + m[i*cols + j]
0x8dc <+88>:  ldr   w0, [sp, #24]      // w0 = j
0x8e0 <+92>:  add   w0, w0, #0x1       // w0 = j + 1
0x8e4 <+96>:  str   w0, [sp, #24]      // j = j + 1
0x8e8 <+100>: ldr   w1, [sp, #24]      // w1 = j
0x8ec <+104>: ldr   w0, [sp]           // w0 = cols
0x8f0 <+108>: cmp   w1, w0             // so sánh j và cols
0x8f4 <+112>: b.lt  0x8a8 <sumMat+36>  // nếu (j < cols) quay lại <sumMat+36>
0x8f8 <+116>: ldr   w0, [sp, #20]      // w0 = i
0x8fc <+120>: add   w0, w0, #0x1       // w0 = i + 1
0x900 <+124>: str   w0, [sp, #20]      // i = i + 1
0x904 <+128>: ldr   w1, [sp, #20]      // w1 = i
0x908 <+132>: ldr   w0, [sp, #4]       // w0 = rows
0x90c <+136>: cmp   w1, w0             // so sánh i và rows
0x910 <+140>: b.lt  0x8a0 <sumMat+28>  // nếu (i < rows) goto <sumMat+28> 
0x914 <+144>: ldr w0, [sp, #28] // w0 = total
0x918 <+148>: add sp, sp, #0x20 // revert stack to prior state
0x91c <+152>: ret // return (total)

Các biến cục bộ i, j và total lần lượt được lưu tại các vị trí trên stack là sp + 20, sp + 24 và sp + 28.
Các tham số đầu vào m, row và cols lần lượt được lưu tại sp + 8, sp + 4 và sp (đỉnh stack).

Với thông tin này, hãy tập trung vào đoạn code chỉ xử lý việc truy cập phần tử (i, j) trong ma trận (từ địa chỉ 0x8a8 đến 0x8d8):

0x8a8 <+36>:   ldr   w1, [sp, #20]       // w1 = i
0x8ac <+40>:   ldr   w0, [sp]            // w0 = cols
0x8b0 <+44>:   mul   w1, w1, w0          // w1 = cols * i

Bộ lệnh đầu tiên này tính giá trị cols * i và lưu vào thanh ghi w1.
Hãy nhớ rằng, với một ma trận tên matrix, biểu thức matrix + i * cols tương đương với &matrix[i].

0x8b4 <+48>:   ldr   w0, [sp, #24]       // w0 = j
0x8b8 <+52>:   add   w0, w1, w0          // w0 = (cols * i) + j
0x8bc <+56>:   sxtw  x0, w0              // x0 = signExtend(cols * i + j)
0x8c0 <+60>:   lsl   x0, x0, #2          // x0 = (cols * i + j) * 4

Bộ lệnh tiếp theo tính (cols * i + j) * 4.
Compiler nhân chỉ số (cols * i + j) với 4 vì mỗi phần tử trong ma trận là một số nguyên 4 byte.
Phép nhân này giúp tính đúng offset trong bộ nhớ.
Lệnh sxtw tại <sumMat+56> mở rộng dấu (sign-extend) giá trị trong w0 thành số nguyên 64-bit, vì giá trị này sẽ được dùng để tính địa chỉ.

Bộ lệnh tiếp theo cộng offset vừa tính vào con trỏ ma trận và dereference để lấy giá trị phần tử (i, j):

0x8c4 <+64>: ldr   x1, [sp, #8]  // x1 = m
0x8c8 <+68>: add   x0, x1, x0    // x0 = m + (cols*i + j)*4 (hay &m[i*cols + j])
0x8cc <+72>: ldr   w0, [x0]      // w0 = m[i*cols + j]
0x8d0 <+76>: ldr   w1, [sp, #28] // w1 = total
0x8d4 <+80>: add   w0, w1, w0    // w0 = total + m[i*cols + j]
0x8d8 <+84>: str   w0, [sp, #28] // total = total + m[i*cols + j]

Lệnh đầu tiên nạp địa chỉ của ma trận m vào thanh ghi x1.
Lệnh add cộng (cols * i + j) * 4 vào địa chỉ m để tính đúng vị trí phần tử (i, j), kết quả lưu vào x0.
Lệnh ldr tiếp theo dereference địa chỉ trong x0 và lưu giá trị m[i * cols + j] vào w0.
Lưu ý: sử dụng w0 (thanh ghi 32-bit) vì phần tử là int (4 byte).

Ba lệnh cuối nạp giá trị hiện tại của total vào w1, cộng với m[i * cols + j], rồi lưu kết quả mới vào total.

Ví dụ truy cập phần tử (1,2) trong ma trận M1 (Hình 3):

matrixArray

Hình 3. Bố trí bộ nhớ của M1 theo thứ tự hàng (row-major order).

Phần tử (1,2) nằm tại địa chỉ M1 + 1 * cols + 2.
Vì cols = 3, nên (1,2) tương ứng với M1 + 5.
Để truy cập phần tử này, compiler nhân 5 với kích thước kiểu int (4 byte), thu được offset M1 + 20, tương ứng với byte a~20~ trong hình.
Dereference vị trí này sẽ lấy được giá trị 5 — đúng là phần tử (1,2) của ma trận.

9.8.2. Ma trận không liên tiếp (Noncontiguous Matrix)

Cách triển khai ma trận không liên tiếp phức tạp hơn một chút.
Hình 4 minh họa cách M2 có thể được bố trí trong bộ nhớ:

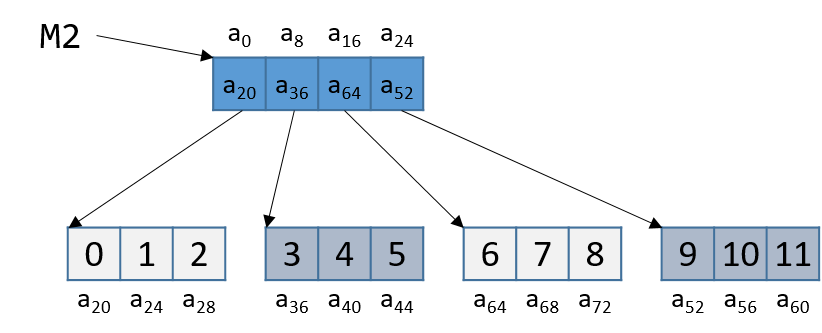
matrixDynamic

Hình 4. Bố trí bộ nhớ không liên tiếp của M2.

Mảng con trỏ trong M2 là liên tiếp.
Mỗi mảng mà M2[i] trỏ tới cũng liên tiếp.
Tuy nhiên, các mảng con này không liên tiếp với nhau trong bộ nhớ.

Vì M2 là mảng con trỏ, mỗi phần tử của M2 chiếm 8 byte.
Ngược lại, mỗi M2[i] là mảng int, nên các phần tử trong mỗi mảng con cách nhau 4 byte.

Hàm sumMatrix trong ví dụ sau nhận:

Tham số đầu tiên: mảng con trỏ tới int (gọi là matrix).
Tham số thứ hai và thứ ba: số hàng và số cột.

int sumMatrix(int **matrix, int rows, int cols) {
    int i, j, total=0;
    for (i = 0; i < rows; i++) {
        for (j = 0; j < cols; j++) {
            total += matrix[i][j];
        }
    }
    return total;
}

Mặc dù hàm này trông gần như giống hệt với hàm sumMat đã trình bày trước đó, nhưng ma trận mà hàm này nhận vào lại bao gồm một mảng liên tiếp các con trỏ.
Mỗi con trỏ chứa địa chỉ của một mảng liên tiếp riêng biệt, tương ứng với một hàng riêng trong ma trận.

Dưới đây là code assembly tương ứng của sumMatrix. Mỗi dòng đều được chú thích bằng tiếng Anh trong bản gốc:

Dump of assembler code for function sumMatrix:
0x920 <+0>:   sub   sp, sp, #0x20         // mở rộng stack thêm 32 byte (frame mới)
0x924 <+4>:   str   x0, [sp, #8]          // lưu matrix tại sp + 8
0x928 <+8>:   str   w1, [sp, #4]          // lưu rows tại sp + 4
0x92c <+12>:  str   w2, [sp]              // lưu cols tại sp (đỉnh stack)
0x930 <+16>:  str   wzr, [sp, #28]        // total = 0 tại sp + 28
0x934 <+20>:  str   wzr, [sp, #20]        // i = 0 tại sp + 20
0x938 <+24>:  b     0x99c <sumMatrix+124> // nhảy tới <sumMatrix+124>
0x93c <+28>:  str   wzr, [sp, #24]        // j = 0 tại sp + 24
0x940 <+32>:  b     0x980 <sumMatrix+96>  // nhảy tới <sumMatrix+96>
0x944 <+36>:  ldrsw x0, [sp, #20]         // x0 = signExtend(i)
0x948 <+40>:  lsl   x0, x0, #3            // x0 = i << 3 (hay i * 8)
0x94c <+44>:  ldr   x1, [sp, #8]          // x1 = matrix
0x950 <+48>:  add   x0, x1, x0            // x0 = matrix + i * 8
0x954 <+52>:  ldr   x1, [x0]              // x1 = matrix[i]
0x958 <+56>:  ldrsw x0, [sp, #24]         // x0 = signExtend(j)
0x95c <+60>:  lsl   x0, x0, #2            // x0 = j << 2 (hay j * 4)
0x960 <+64>:  add   x0, x1, x0            // x0 = matrix[i] + j * 4
0x964 <+68>:  ldr   w0, [x0]              // w0 = matrix[i][j]
0x968 <+72>:  ldr   w1, [sp, #28]         // w1 = total
0x96c <+76>:  add   w0, w1, w0            // w0 = total + matrix[i][j]
0x970 <+80>:  str   w0, [sp, #28]         // total = total + matrix[i][j]
0x974 <+84>:  ldr   w0, [sp, #24]         // w0 = j
0x978 <+88>:  add   w0, w0, #0x1          // w0 = j + 1
0x97c <+92>:  str   w0, [sp, #24]         // j = j + 1
0x980 <+96>:  ldr   w1, [sp, #24]         // w1 = j
0x984 <+100>: ldr   w0, [sp]              // w0 = cols
0x988 <+104>: cmp   w1, w0                // so sánh j với cols
0x98c <+108>: b.lt  0x944 <sumMatrix+36>  // nếu (j < cols) quay lại <sumMatrix+36>
0x990 <+112>: ldr   w0, [sp, #20]         // w0 = i
0x994 <+116>: add   w0, w0, #0x1          // w0 = i + 1
0x998 <+120>: str   w0, [sp, #20]         // i = i + 1
0x99c <+124>: ldr   w1, [sp, #20]         // w1 = i
0x9a0 <+128>: ldr   w0, [sp, #4]          // w0 = rows
0x9a4 <+132>: cmp   w1, w0                // so sánh i với rows
0x9a8 <+136>: b.lt  0x93c <sumMatrix+28>  // nếu (i < rows) quay lại <sumMatrix+28>
0x9ac <+140>: ldr   w0, [sp, #28]         // w0 = total
0x9b0 <+144>: add   sp, sp, #0x20         // khôi phục stack
0x9b4 <+148>: ret                         // trả về total

Tương tự như trước, các biến i, j và total lần lượt nằm tại sp + 20, sp + 24 và sp + 28.
Các tham số đầu vào matrix, row và cols lần lượt nằm tại sp + 8, sp + 4 và sp (đỉnh stack).

Hãy tập trung vào đoạn code xử lý việc truy cập phần tử (i, j) — tức matrix[i][j] — từ địa chỉ 0x944 đến 0x970:

0x944 <+36>:   ldrsw  x0, [sp, #20]          // x0 = signExtend(i)
0x948 <+40>:   lsl    x0, x0, #3             // x0 = i << 3 (hay i * 8)
0x94c <+44>:   ldr    x1, [sp, #8]           // x1 = matrix
0x950 <+48>:   add    x0, x1, x0             // x0 = matrix + i * 8
0x954 <+52>:   ldr    x1, [x0]               // x1 = matrix[i]

Năm lệnh trên tính toán matrix[i] hay *(matrix + i).
Vì matrix[i] chứa một con trỏ, i trước tiên được chuyển thành số nguyên 64-bit.
Sau đó, compiler nhân i với 8 bằng phép dịch trái (lsl), rồi cộng kết quả vào địa chỉ matrix để tính offset chính xác (nhớ rằng con trỏ chiếm 8 byte).
Lệnh tại <sumMatrix+52> dereference địa chỉ vừa tính để lấy giá trị matrix[i].

Vì matrix là mảng các con trỏ int, phần tử tại matrix[i] bản thân nó là một con trỏ int.
Phần tử thứ j trong matrix[i] nằm tại offset j × 4 trong mảng matrix[i].

Bộ lệnh tiếp theo trích xuất phần tử thứ j trong mảng matrix[i]:

0x958 <+56>:   ldrsw  x0, [sp, #24]     // x0 = signExtend(j)
0x95c <+60>:   lsl    x0, x0, #2        // x0 = j << 2 (hay j * 4)
0x960 <+64>:   add    x0, x1, x0        // x0 = matrix[i] + j * 4
0x964 <+68>:   ldr    w0, [x0]          // w0 = matrix[i][j]
0x968 <+72>:   ldr    w1, [sp, #28]     // w1 = total
0x96c <+76>:   add    w0, w1, w0        // w0 = total + matrix[i][j]
0x970 <+80>:   str    w0, [sp, #28]     // total = total + matrix[i][j]

Lệnh đầu tiên nạp j vào x0 và sign-extend.
Lệnh lsl nhân j với 4 và lưu vào x0.
Lệnh add cộng giá trị này vào địa chỉ matrix[i] để lấy địa chỉ &matrix[i][j].
Lệnh tại <sumMatrix+68> dereference địa chỉ này để lấy giá trị matrix[i][j] và lưu vào w0.
Cuối cùng, các lệnh từ <sumMatrix+72> đến <sumMatrix+80> sẽ cộng giá trị total với matrix[i][j] và cập nhật biến total bằng tổng vừa tính được.

Ví dụ truy cập M2[1][2] (hình minh họa bên dưới):

matrixDynamic

Giả sử M2 bắt đầu tại địa chỉ bộ nhớ a~0~.
Compiler trước tiên tính địa chỉ của M2[1] bằng cách nhân 1 với 8 (sizeof(int *)) và cộng vào địa chỉ của M2 (a~0~), thu được địa chỉ mới a~8~.
Dereference địa chỉ này sẽ cho ra địa chỉ mà M2[1] trỏ tới, tức a~36~.

Tiếp theo, compiler nhân chỉ số 2 với 4 (sizeof(int)) và cộng kết quả (8) vào a~36~, thu được địa chỉ cuối cùng là a~44~.
Dereference địa chỉ a~44~ này sẽ cho giá trị 5.
Quả thật, phần tử trong [DynamicMatrix6a64repro] tương ứng với M2[1][2] có giá trị là 5.

Đắm mình vào hệ thống - Dive into Systems

9.8. Ma trận (Matrices)

9.8.1. Mảng hai chiều liên tiếp (Contiguous Two-Dimensional Arrays)

9.8.2. Ma trận không liên tiếp (Noncontiguous Matrix)